
Bevezetés a funkciókba R
A függvény az utasítások halmaza, amely bármilyen logikai feladat elvégzésére és végrehajtására szolgál. A Function néhány bemeneti paramétert igényel, amelyek argumentumnak tekinthetők a feladat végrehajtásához. A funkciók segítségével a kódot egyszerűbb darabbá oszthatják, mivel logikusan hangolják el, ami könnyebben olvasható és érthető. Ebben a témában megismerjük az R funkcióit.
Hogyan írhatunk R funkciókat?
A függvény R-beírásához itt van a szintaxis:
Fun_name <- function (argument) (
Function body
)
Itt láthatjuk, hogy az „R” -ben a „függvény” -hez tartozó fenntartott szót használjuk bármilyen funkció meghatározására. A függvény inputot vesz fel, argumentumok formájában. A függvénytest logikai utasítások halmaza, amelyeket argumentumokkal hajtanak végre, majd visszaadják a kimenetet. A „Fun_name” a függvénynek adott név, amelyen keresztül az R program bárhol meghívható.
Lássunk egy példát, amely sokkal tisztább lesz a funkció funkciójának megértésében R-ben.
R kód
Multi <- function(x, y) (
# function to print x multiply y
result <- x*y
print(paste(x, "Multiply", y, "is", result))
)
Kimenet:
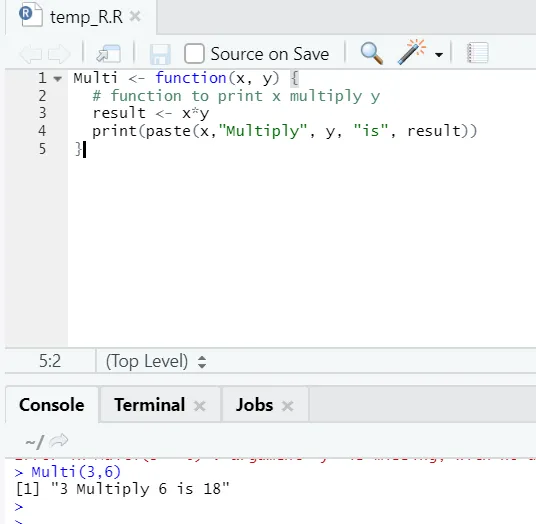
Itt létrehoztuk a „Multi” funkciónevet, amely két argumentumot vesz bemenetként és biztosítja a szorzott kimenetet. Az első argumentum x, a második argumentum pedig y. Mint láthatja, a funkciót „Multi” néven hívtuk. Itt, ha valaki akar, az argumentumokat az alapértelmezett értékre is beállíthatja.
Különböző típusú funkciók az R-ben
Különböző R funkciók szintaxissal és példákkal (beépített, matematikai, statisztikai stb.)
1) Beépített funkció -
Ezek azok a funkciók, amelyek az R-vel egy adott feladat megoldására szolgálnak, amikor argumentumot vesznek bemenetként, és az adott bemeneten alapuló outputot adnak. Itt tárgyaljuk az R néhány fontos általános funkcióját:
a) Rendezés: Az adatok lehetnek növekvő vagy csökkenő sorrendben. Az adat lehet, hogy folytatódik-e a változó vagy faktor-változó.
Szintaxis:

Itt található a paraméterek magyarázata:
- x: Ez a folyamatos változó vagy tényező változó vektorja
- csökkenő: Ezt igaz / hamis értékre lehet állítani a növekvő vagy csökkenő sorrend vezérlésére. Alapértelmezés szerint FALSE.
- utoljára: Ha a vektor NA-értékekkel rendelkezik, akkor utolsónak kell-e hagyni, vagy sem
R-kód és kimenet:
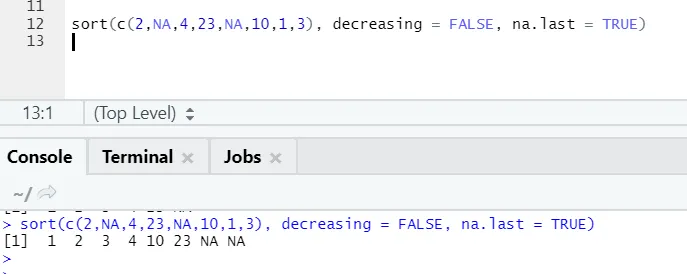
Itt észrevehető, hogy a „NA” értékek hogyan igazodnak a végéhez. Mivel a na.last = True paraméter igaz volt.
b) Seq: A megadott számok sorozatát generálja két megadott szám között.
Szintaxis
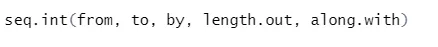
Itt található a paraméterek magyarázata:
- from, a szekvencia kezdő és záró értéke.
- Írta: Növelés / távolság két egymást követő szám között egymás után
- length.out: a szekvencia szükséges hossza.
- Along.with: Az érvelés hosszától függ
R-kód és kimenet:
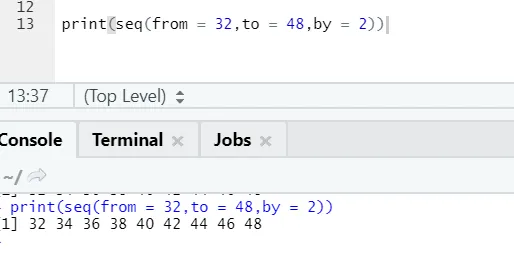
Itt észrevehető a generált szekvencia 2-es növekedése, mivel a 2-vel definiálva van.
c) Toupper, tolower: A két függvény: toupper és tolower azok a függvények, amelyeket a karakterláncon alkalmaznak, hogy megváltoztassák a betűk mondatban mondatát.
R-kód és kimenet:
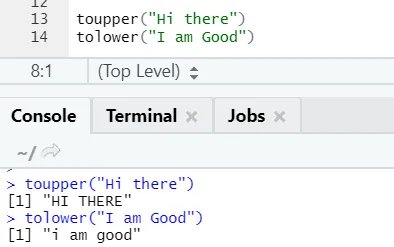
Észrevehető, hogy a betűk esete megváltozik, amikor a funkcióra alkalmazzák.
d) Rnorm: Ez egy beépített funkció, amely véletlenszerű számokat generál.
R-kód és kimenet:
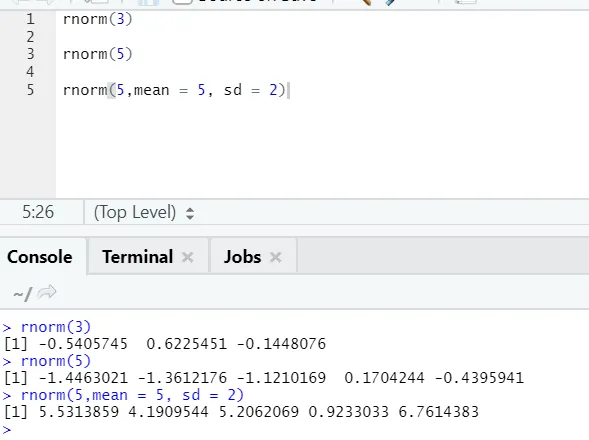
Az rnorm függvény veszi az első érvet, amely azt mondja, hogy hány számot kell generálni.
e) Rep: Ez a funkció a megadott számú alkalommal replikálja az értéket.
R szintaxis: rnorm (x, n)
Itt x replikációs értéket jelent, n pedig replikálási hányszor jelöli.
R-kód és kimenet:
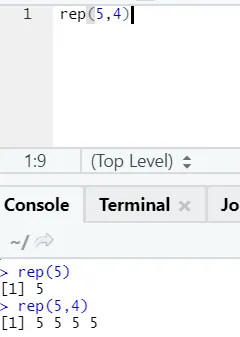
f) Beillesztés: Ez a funkció a karakterláncokat összekapcsolja, a közöttük lévő speciális karakterekkel együtt.
szintaxis
paste(x, sep = “”, collapse = NULL)
R kód
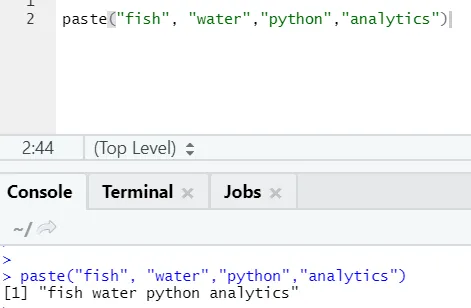
paste("fish", "water", sep=" - ")
R kimenet:
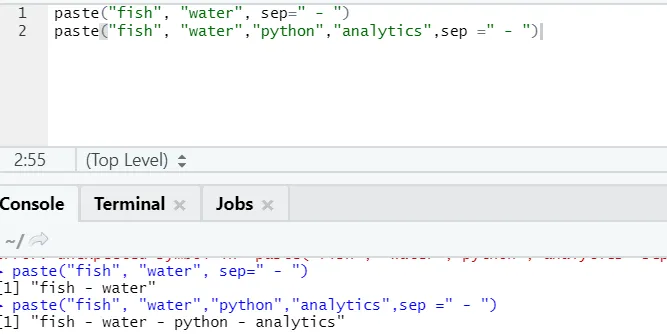
Mint látható, több mint két karakterláncot is beilleszthetünk. Sep az a specifikus karakter, amelyet a karakterláncok között adtunk hozzá. Alapértelmezés szerint a sep szóköz.
Még egy hasonló funkció létezik, mint ez, amelyet mindenkinek tudnia kell, a paste0.
A paste0 (x, y, collapse) függvény hasonlóan működik, mint a paste (x, y, sep = “”, összecsukás)
Kérjük, olvassa el az alábbi példát:
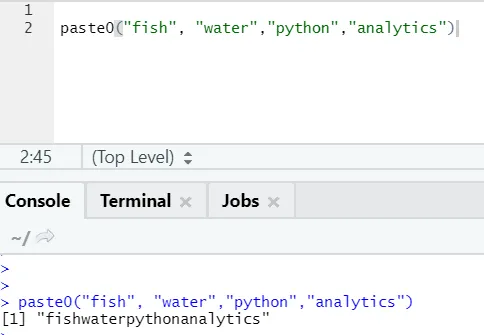
Egyszerű szavakkal, a paste és paste összefoglalására:
A Paste0 gyorsabb, mint a paszta, amikor a vonóságok összekapcsolására szolgál elválasztó nélkül. Mivel a paszta mindig a „sep” kifejezést keresi, amely alapértelmezés szerint helyet foglal el.
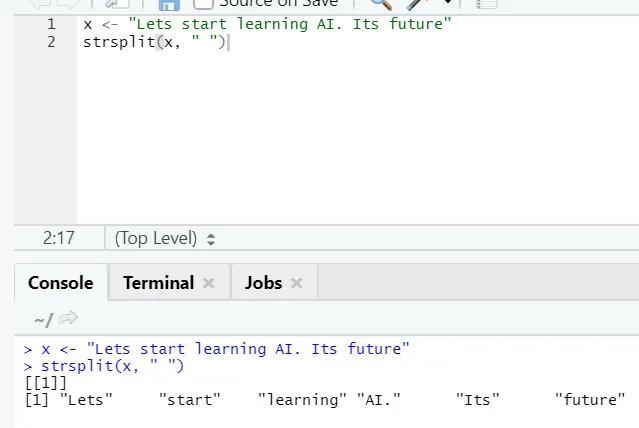
g) Strsplit: Ez a funkció a húr felosztására szolgál. Lássuk az egyszerű eseteket:
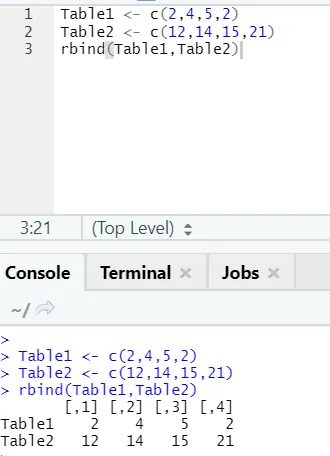
h) Rbind: Az rbind funkció segíti az azonos oszlopszámú vektorok fésülését, egymással szemben.
Példa
i) cbind: Ez a vektorokat egyesíti azonos számú sorral, egymás mellett.
Példa
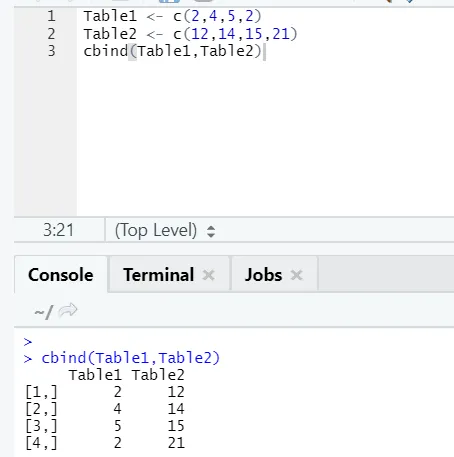
Ha a sorok száma nem egyezik, akkor az alább látható hiba található:

A cbind és az rbind egyaránt segít az adatkezelésben és az átalakításban.
2) Matematikai funkció -
Az R a matematikai funkciók széles skáláját kínálja. Nézzük meg néhányat részletesebben:
a) Sqrt: Ez a függvény kiszámítja egy szám vagy numerikus vektor négyzetgyökét.
R-kód és kimenet:
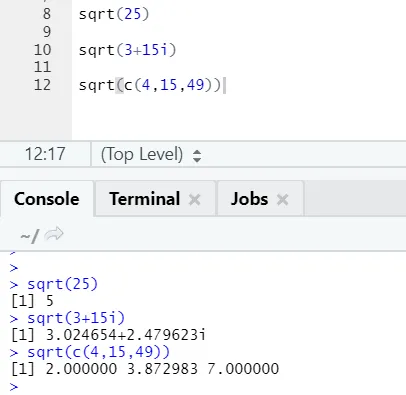
Látható, hogyan lehet kiszámítani egy szám, komplex szám és a numerikus vektor sorozatának négyzetgyökét.
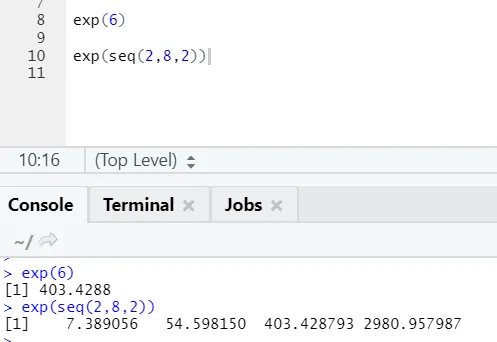
b) Exp: Ez a funkció kiszámítja egy szám vagy numerikus vektor exponenciális értékét.
R-kód és kimenet:
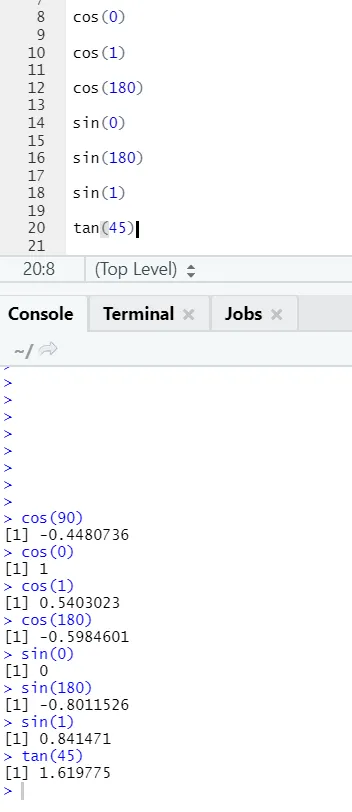
c) Cos, Sin, Tan: Ezek itt R-ben megvalósított trigonometria függvények.
R-kód és kimenet:
d) Abs: Ez a függvény egy szám abszolút pozitív értékét adja vissza.
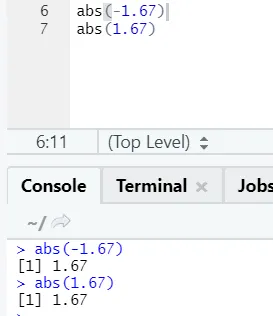
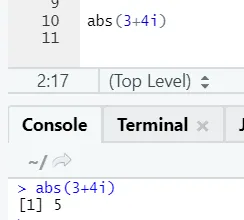
Mint láthatja, egy szám negatív vagy pozitív visszatér abszolút formájában. Nézzük meg egy komplex számhoz:
e) Napló: Ennek célja egy szám logaritmusának megkeresése.
Az alábbiakban bemutatott példa:
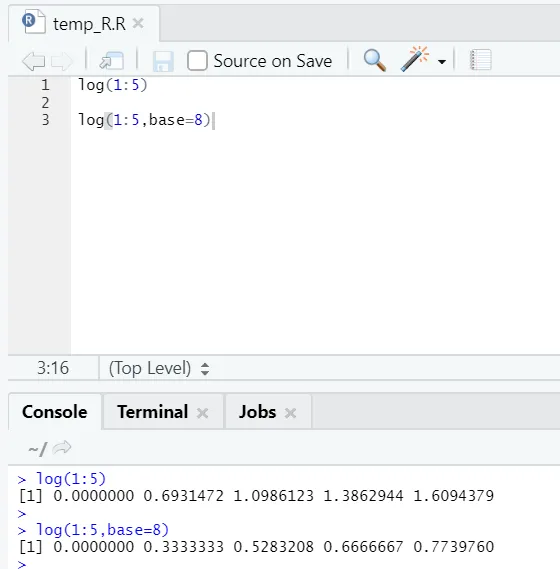
Itt rugalmasságot kap az alap megváltoztatása, a követelményeknek megfelelően.
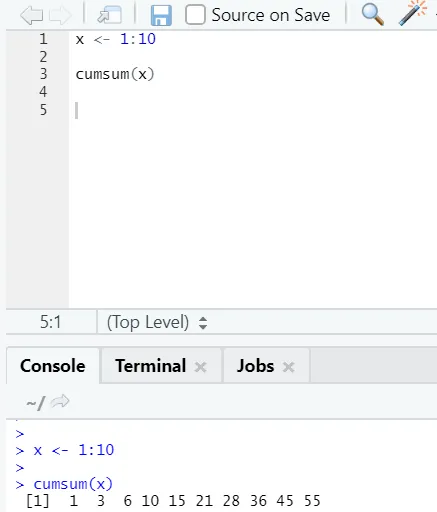
f) Cumsum: Ez egy matematikai függvény, amely halmozott összegeket ad. Itt van az alábbi példa:
g) Cumprod: A Cumsum matematikai függvényéhez hasonlóan olyan cumprod van, ahol kumulatív szorzás történik.
Kérjük, olvassa el az alábbi példát:
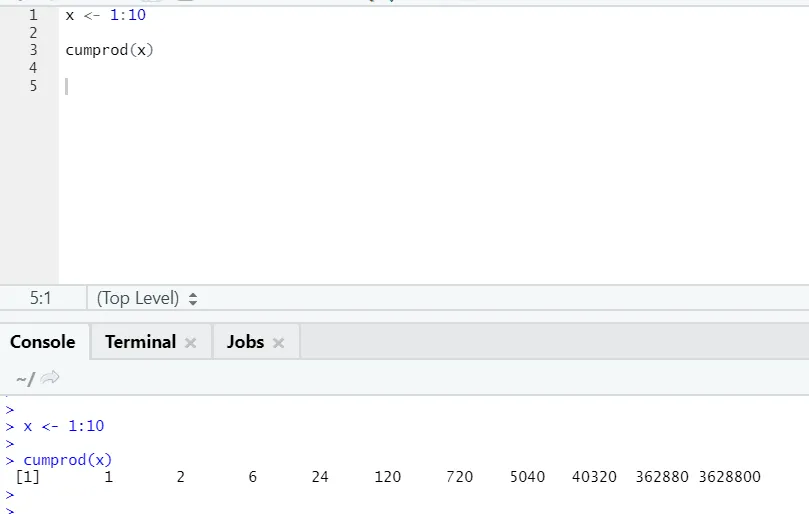
h) Max, Min: Ez segít megtalálni a maximális / minimális értéket a számkészletben. Lásd alább az ehhez kapcsolódó példákat:
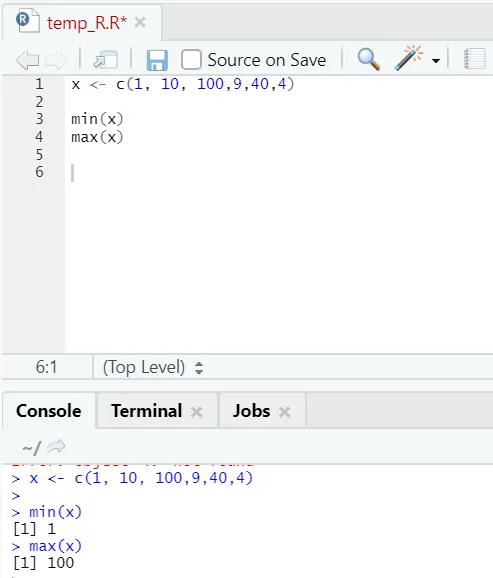
i) Mennyezet: A mennyezet egy matematikai függvény, amely a megadottnál nagyobb egész számot adja vissza.
Nézzünk egy példát:
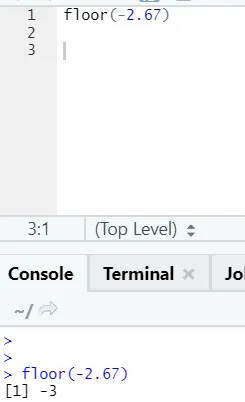
mennyezet (2, 67)
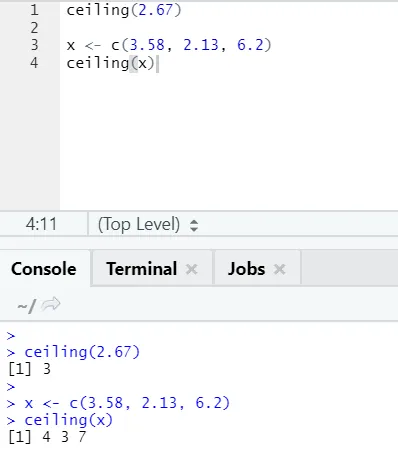
Mint észrevehetjük, a felső határt számra és egy listára egyaránt alkalmazzuk, és a kimenő output a következő nagyobb egész szám közül a legkisebb.
j) Padló: A padló egy matematikai függvény, amely a megadott szám legkisebb egész számát adja vissza.
Az alább látható példa segít jobban megérteni:
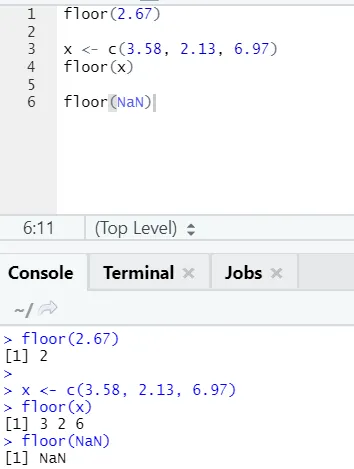
Ugyanígy működik a negatív értékeknél is. Kérem nézze meg:
3) Statisztikai funkciók -
Ezek a függvények leírják a kapcsolódó valószínűség-eloszlást.
a) Medián: Ez számította a mediánt a számsorból.
Szintaxis
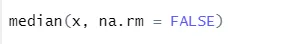
R-kód és kimenet:
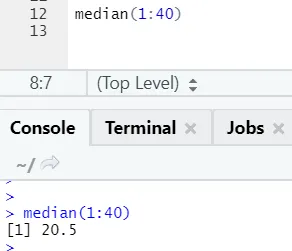
b) Dnorm: Ez a normál eloszlásra vonatkozik. A dnor függvény a valószínűség-sűrűség függvény értékét adja vissza a normál eloszláshoz, megadva az x, μ és σ paramétereket.
R-kód és kimenet:
c) Cov: A kovariancia megmutatja, ha két vektor pozitív, negatív vagy teljesen nem rokon.
R kód
x_new = c(1., 5.5, 7.8, 4.2, -2.7, -5.5, 8.9)
y_new = c(0.1, 2.0, 0.8, -4.2, 2.7, -9.4, -1.9)
cov(x_new, y_new)
R kimenet:
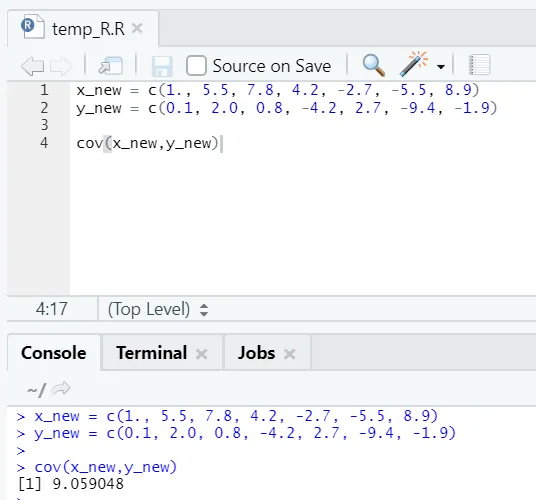
Mint láthatja, két vektor pozitív kapcsolatban áll, ami azt jelenti, hogy mindkét vektor azonos irányba mozog. Ha a kovariancia negatív, az azt jelenti, hogy x és y fordítva vannak, és ellentétes irányba haladnak.
d) Cor: Ez a vektorok közötti korreláció megtalálásának funkciója. Valójában megadja a két vektor közötti asszociációs tényezőt, az úgynevezett „korrelációs együtthatót”. A korreláció fokozási tényezőt ad a kovariancia fölött. Ha két vektor pozitív korrelációban van, akkor a korreláció azt is megmutatja, mennyi kiterjedésük van pozitív kapcsolatban.
A három módszer típusa, amely felhasználható korreláció megállapítására két vektor között:
- Pearson-korreláció
- Kendall-korreláció
- A Spearman korreláció
Egyszerű R formátumban a következőképpen néz ki:
cor(x, y, method = c("pearson", "kendall", "spearman"))
Itt x és y vektorok.
Lássuk a beépített adatkészlet közötti korreláció gyakorlati példáját.
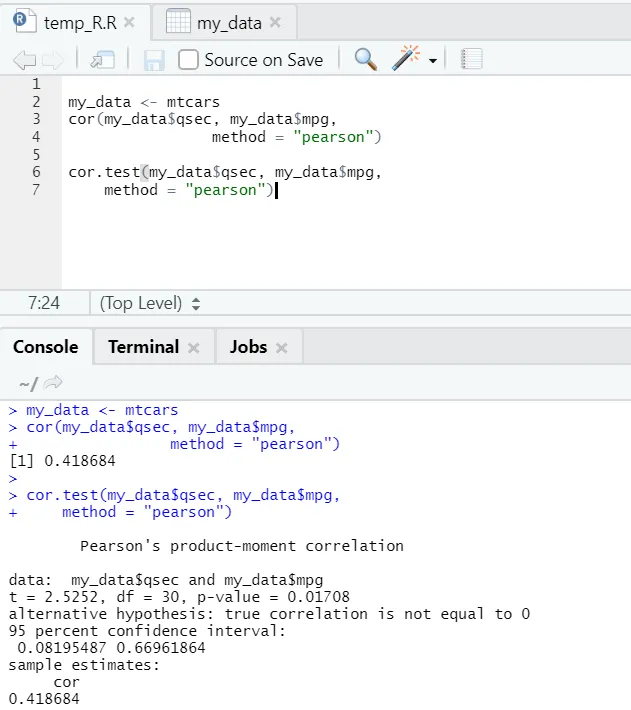
Tehát itt látható a „cor ()” függvény 0, 41 korrelációs együtthatót adva a „qsec” és az „mpg” között. Ugyanakkor bemutattak még egy függvényt, azaz „cor.test ()”, amely nemcsak a korrelációs együtthatót, hanem a hozzá tartozó p-értéket és t-értéket is megmutatja. Az értelmezés sokkal könnyebbé válik a cor.test funkcióval.
Hasonló lehet a másik két korrelációs módszerrel:
A Pearson-módszer R kódja:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " pearson ")
cor.test(my_data$qsec, my_data$mpg, method = " pearson")
A Kendall-módszer R kódja:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " kendall")
cor.test(my_data$qsec, my_data$mpg, method = " kendall")
R kód a Spearman módszerhez:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = "spearman")
cor.test(my_data$qsec, my_data$mpg, method = "spearman")
A korrelációs együttható -1 és 1 között van.
Ha a korrelációs együttható negatív, az azt jelenti, hogy amikor x növekszik, akkor az y csökken.
Ha a korrelációs együttható nulla, ez azt jelenti, hogy nincs kapcsolat x és y között.
Ha a korrelációs együttható pozitív, akkor ez azt jelenti, hogy amikor x növekszik, akkor az y szintén növekszik.
e) T-teszt: A T-teszt megmondja, hogy két adatkészlet ugyanazon (feltételezve) normál eloszlásból származik-e vagy sem.
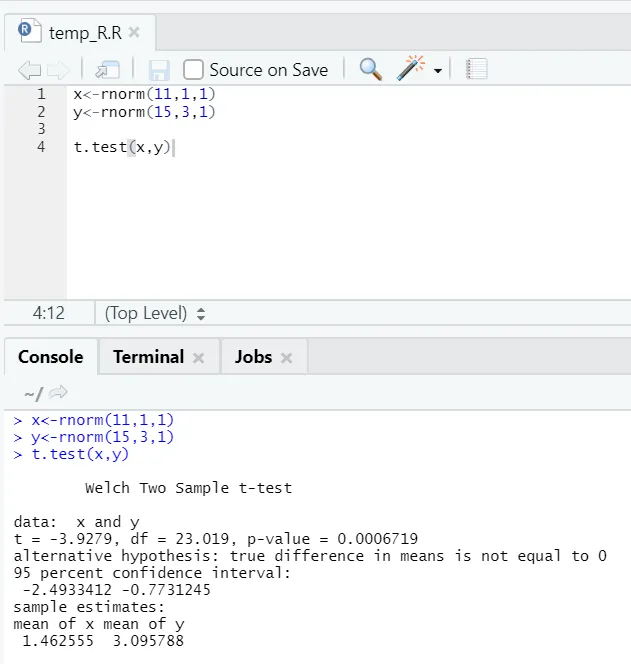
Itt el kell utasítani a nulla hipotézist, miszerint a két átlag egyenlő, mivel a p-érték kisebb, mint 0, 05.
Ez a bemutatott példány típusa: páratlan adatkészletek egyenlőtlen eltérésekkel. Hasonlóképpen kipróbálható a páros adatkészlettel is.
f) Egyszerű lineáris regresszió: Ez megmutatja az előrejelző / független és a válasz / függő változó közötti kapcsolatot.
Egy egyszerű gyakorlati példa lehet egy ember súlyának előrejelzése, ha a magasság ismert.
R szintaxis
lm(formula, data)
A képlet a kimeneti, azaz y és az iex bemeneti változó közötti viszonyt ábrázolja. Az adatok azt az adatkészletet képviselik, amelyre a képletet alkalmazni kell.
Lássuk egy gyakorlati példát, ahol a alapterület a bemeneti változó, a bérleti díj pedig a kimeneti változó.
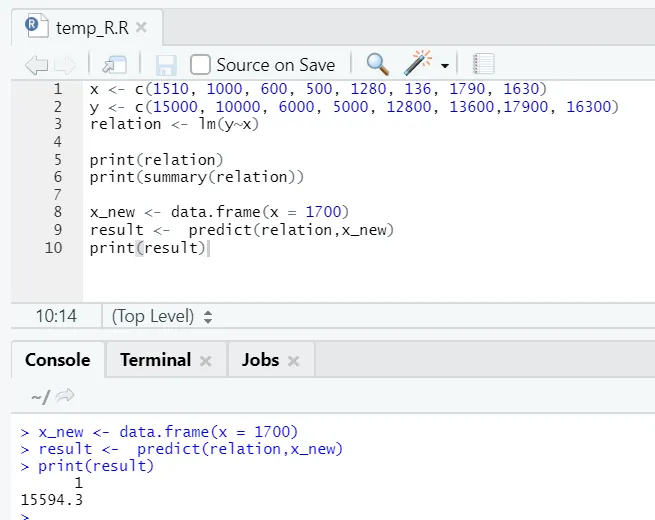
x <- c (1510, 1000, 600, 500, 1280, 136, 1790, 1630)
y <- c (15000, 10000, 6000, 5000, 12800, 13600, 17900, 16300)
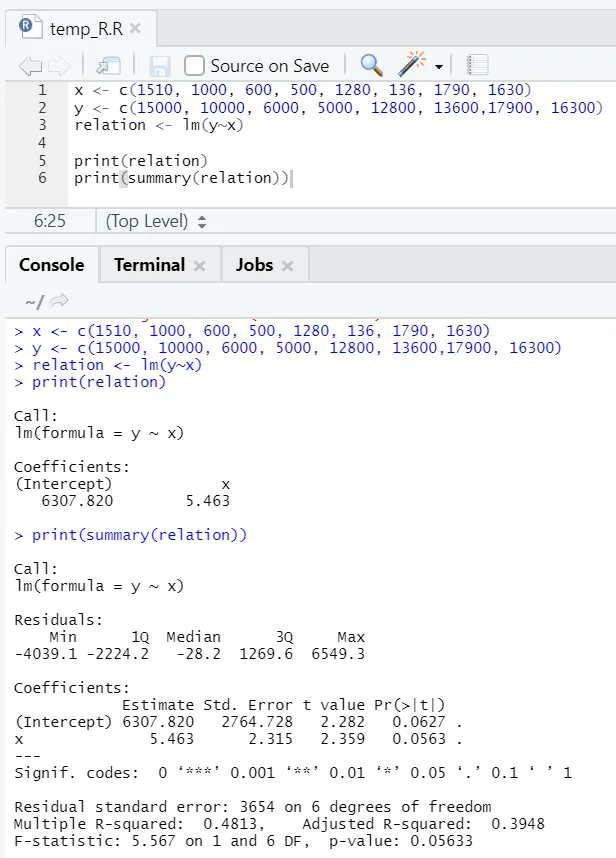
Itt a P-érték legalább 5%. Ezért a nullhipotézist nem lehet elutasítani. A földterület és a bérleti kapcsolat kapcsolatának bizonyítására nincs jelentősége.
Itt az R-négyzet értéke 0, 4813. Ez azt jelenti, hogy a kimeneti változó varianciájának csak 48% -a magyarázható a bemeneti változóval.
Tegyük fel, hogy most meg kell becsülnünk a padlóterület értékét, a fent felszerelt modell alapján.
R kód
x_new <- data.frame(x = 1700)
result <- predict(relation, x_new)
print(result)
R kimenet:
A fenti R kód végrehajtása után a kimenet a következőképpen néz ki:
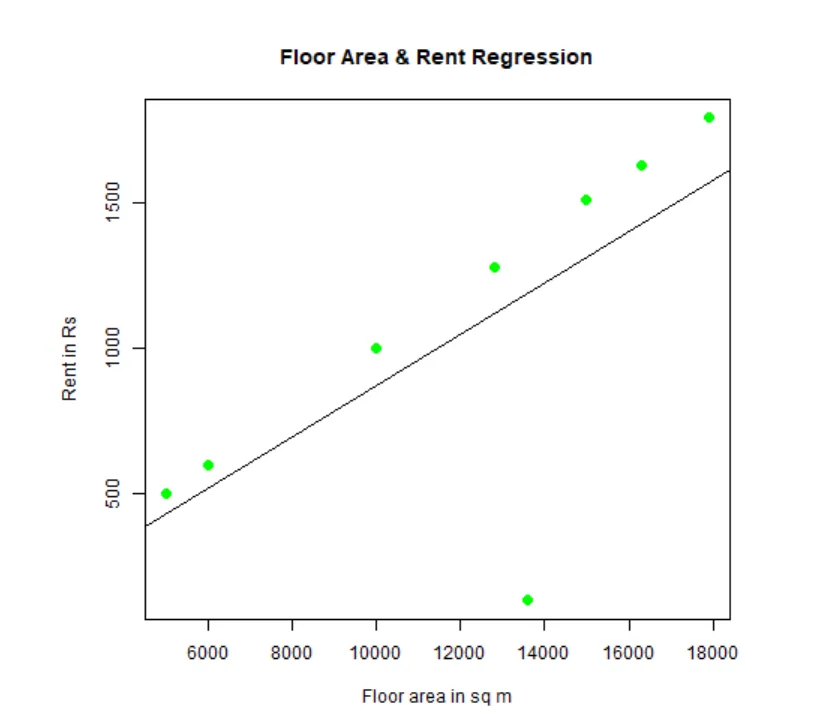
A regresszió illeszthető és megjeleníthető. Íme az R kód:
# Adjon nevet a png chart fájlnak.
png(file = "LinearRegressionSample.png.webp")
# Rajzolja meg a diagramot.
plot(y, x, col = "green", main = "Floor Area & Rent Regression",
abline(lm(x~y)), cex = 1.3, pch = 16, xlab = "Floor area in sq m", ylab = "Rent in Rs")
# Mentse el a fájlt.
dev.off()
Ezt a „LinearRegressionSample.png.webp” gráfot a jelenlegi munkakönyvtárban kell létrehozni.
g) Chi-négyzet teszt
Ez egy statisztikai függvény R-ben. Ez a teszt jelentősége annak bizonyítására szolgál, hogy fennáll-e korreláció két kategorikus változó között.
Ez a teszt ugyanúgy működik, mint bármely más statisztikai teszt, amely p-értéken alapult, elfogadható vagy elutasítható a nullhipotézis.
R szintaxis
chisq.test(data), /code>
Lássuk ennek egy gyakorlati példáját.
R kód
# Töltse be a könyvtárat.
library(datasets)
data(iris)
# Hozzon létre egy adatkeretet a fő adatkészletből.
iris.data <- data.frame(iris$Sepal.Length, iris$Sepal.Width)
# Készítsen egy táblát a szükséges változókkal.
iris.data = table(iris$Sepal.Length, iris$Sepal.Width)
print(iris.data)
# Végezze el a Chi-Square tesztet.
print(chisq.test(iris.data))
R kimenet:
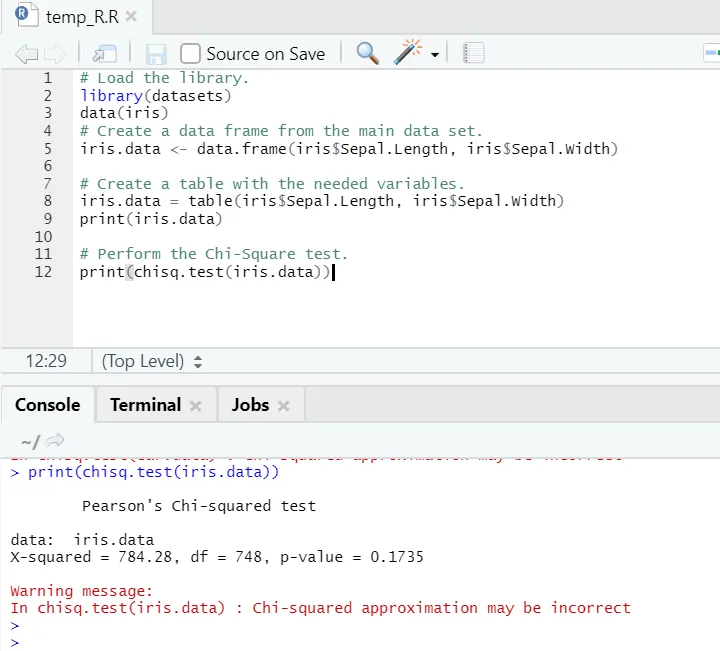
Mint látható, a chi-négyzet teszt írisz adatkészlettel történt, figyelembe véve annak két változóját: „Sepal. Hossz ”és„ Sepal.Width ”.
A p-érték nem kevesebb, mint 0, 05, ezért a két változó között nincs korreláció. Vagy azt mondhatjuk, hogy ez a két változó nem függ egymástól.
Következtetés
Az R funkciók egyszerűek, könnyen illeszthetők, könnyen megfoghatók és mégis nagyon erősek. Számos olyan funkciót láthattunk, amelyeket az alapok részeként használunk R-ben. Ha egyszer megismerkednek ezekkel a fentebb tárgyalt funkciókkal, meg lehet vizsgálni a függvények más fajtáit is. A funkciók segítenek abban, hogy a kód egyszerűen és tömören futjon. A funkciók beépíthetők vagy felhasználó által definiálhatók, mindegyik a probléma megoldásának szükségességétől függ. A funkciók jó formát adnak a program számára.
Ajánlott cikkek
Ez egy útmutató az R. funkcióihoz. Itt megvitatjuk, hogyan kell írni a függvényeket R-ben és a különféle típusú funkciókat az R-ben szintaxissal és példákkal. A következő cikkben további információkat is megnézhet -
- R karakterlánc funkciók
- SQL karakterlánc-funkciók
- T-SQL karakterlánc funkciók
- PostgreSQL karakterlánc funkciók