Komplex számok a MATLAB-ban Hogyan generálhatunk komplex számot?

Bevezetés a komplex számokba a MATLAB-ban

A komplex számok a valós számok és a képzeletbeli számok kombinációját jelentik p + qi formájában, ahol p és q a valós számok és i a képzeletbeli szám. Egy képzeletbeli számot definiálunk, ahol i a 2 = -1 egyenlet eredménye. Használhatjuk i vagy j jelöléssel a képzeletbeli egységeket. Mivel a matematikai számításokban komplex számokat használnak, és a Matlabot főként a matematikai számítások elvégzésére használják. Tehát a komplex számok fontos részét képezik a Matlab tanulásának.

Komplex számok generálása a MATLAB-ban

Komplex számok létrehozhatók vagy deklarálhatók a Matlabban egy 'összetett' függvény segítségével. Összetett számokat is létrehozhatunk bármely negatív szám négyzetgyökével. A Matlabban az i vagy a j használatával jelölhetjük a komplex szám képzeletbeli részét.

Példák

X = 4 + 5i

Itt X egy komplex szám, amely 2 részből áll, azaz a valódi és a képzeletből. 4 a valós rész és 5 a képzeletbeli rész. A Matlab függvényei segítségével megtalálhatjuk a valódi és a képzeletbeli részeket.

a = valós (X) = 4 (Ez adja a komplex szám valós részét)
b = imag (X) = 5 (Ez adja a komplex szám képzeletbeli részét)
komplex (6, 7) = 6 + 7i (ezt a funkciót komplex szám létrehozására használják)

A Matlab-ban összetett tömböket is létrehozhatunk, amelyek a komplex függvények felhasználásával is deklarálhatók.

a = komplex (x, y)

Vannak bizonyos feltételek x-re és y-ra, amelyeket követnünk kell, mint például az x-nek és y-nek nem szabad egy vagy kettõsnek lennie. Komplex skalár hozható létre, ha két bemenet jellegű skaláris, például,

X = komplex (5, 3)
X = 5, 0000 + 3, 0000i

Hasonlóképpen, összetett vektor is létrehozható, ha két bemenetünk van vektorként.

X = Uint8 ((4; 5; 6; 7));
Y = Uint8 ((3; 5; 1; 2));
a = komplex (X, Y)

4 + 3i

5 + 5i

6 + 1i

7 + 2i

Készíthetünk komplex számot, amelynek csak egy skalárja van,

X = komplex (10)
X = 10, 0000 + 0, 0000i

Vannak bizonyos feltételek, amelyeket a bemeneti és a kimeneti argumentumoknak követniük kell,

A bemeneti argumentumok valós és képzeletbeli részeket tartalmaznak, például x bármilyen y-t. x és y legyen skalár, vektor, többdimenziós tömb vagy mátrix a MATLAB-ban. x és y méretének azonosnak kell lennie. Ugyanazon adattípussal kell rendelkezniük, de néhány kivételtől eltekintve pl. A dupla használható az egyszeri és az egész kombinálható a duplával, amely skaláris.

A tömb kimenete lehet vektor, skalár, mátrix vagy többdimenziós tömb, a bemeneti argumentumoktól függően. A kimenet méretének meg kell egyeznie a bemenet méretével. Ha a bemeneti argumentumok eltérő adattípusokat tartalmaznak, akkor a kimenetet a következő határozza meg:

Ha valamelyik bemeneti argumentum jellegű, akkor a kimenetnek is egyedinek kell lennie.
Ha az egyik bemeneti argumentum egész számú, akkor a kimenetnek egész adattípusnak kell lennie.

Isreal függvénnyel ellenőrizhetjük, hogy a mátrix valódi vagy képzeletbeli.

Kód:

X = (2+i, 1); Isreal(X)

Kimenet:

Kód:

Isreal (X (2))

Kimenet:

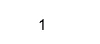
A valódi és a képzeletbeli részek kibontásához használhatunk valódi és imag funkciókat a Matlabban,

Kód:

real(X)

Kimenet:

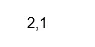
Kód:

imag(X)

Kimenet:

Komplex számok működése és funkciói a MATLAB-ban

Számos művelet és funkció végrehajtható komplex számok segítségével a Matlab-ban

abs: Ezt a funkciót használjuk bármilyen komplex szám modulusának p + qi formájában történő megkeresésére. abs (2 + 3i) = (2 2 + 3 2) = (13) 0, 5 négyzetgyöke
szög: a komplex szám fázisszögeinek meghatározása.

Van néhány tipp, amelyet be kell tartani a komplex számok megfelelő működéséhez a Matlabban, például:

Kerüljük az i és j használatát a változónevek részeként, mivel ezeket használják a komplex szám képzeletbeli részeinek megjelölésére.
Kerüljük el a j vagy i használatát, ha a képzeletbeli része 1. Ehelyett használhatjuk az 1j vagy az 1i értéket.
Összetett függvényt hozhatunk létre a Matlab-ban, ha i és j változónevekként vannak használva, a bemeneti argumentumok nem egy- vagy kettõs típusúak, és a képzeletbeli rész nulla.

Következtetés

A komplex számokat a matematikai vagy a mérnöki területen használják. Számos valós vagy gyakorlati alkalmazás leírható a komplex számok képzeletbeli részének felhasználásával. Tehát fontos az összetett számok használatának és alkalmazásának megértése a különféle platformokon, különösen akkor, ha bármilyen fizikai vagy matematikai területtel foglalkozik.

Ajánlott cikkek

Ez egy útmutató a komplex számokhoz a MATLAB-ban. Itt tárgyaljuk a bevezetést és a komplex számgenerálást a Matlabban, beleértve annak példáit a működéssel és a funkcióval. A következő cikkeket is megnézheti további információkért -