Az átlagos eltolási algoritmus meghatározása
Az átlagos Shift algoritmus felügyelet nélküli tanulás alá tartozik, amelyet Clustering algoritmusnak tekintünk. Az Mean Shift algoritmus ideológiája az, hogy az adatpontokat iterációs úton rendeli a klaszterekhez úgy, hogy elmozdul a legmagasabb sűrűségű pont felé (Mód). Az átlagos eltolódás logika a Kernel sűrűségbecslés KDE néven ismeretes koncepcióján alapszik.
Átlagos eltolási algoritmus klaszterezés
Egy felügyelet nélküli tanulási technika, amelyet Fukunaga és Hostetler fedez fel klaszterek keresésére:
- Az átlagos eltolást módkeresési algoritmusnak is nevezik, amely az adatpontokat a klaszterekhez rendeli úgy, hogy az adatpontokat a nagy sűrűségű régió felé tolja. Az adatpontok legnagyobb sűrűségét modellnek nevezik a régióban. Az Mean Shift algoritmus alkalmazásokat széles körben használ a számítógépes látás és a kép szegmentálás területén.
- A KDE módszer az adatpontok eloszlásának becslésére. Úgy működik, hogy kernelt helyez az egyes adatpontokra. A matematika szempontjából a kernel egy olyan súlyozó függvény, amely az egyes adatpontokra súlyokat fog alkalmazni. Az összes kernel hozzáadása valószínűséget generál.
A rendszermag-funkciónak teljesítenie kell a következő feltételeket:
- Az első követelmény annak biztosítása, hogy a kernel sűrűségének becslése normalizálódjon.
- A második követelmény, hogy a KDE jól kapcsolódjon a tér szimmetriájához.
Két népszerű kernelfunkció
Az alábbiakban a benne használt két népszerű kernelfunkció van:
- Lapos kernel
- Gauss-kernel
- Az alkalmazott Kernel param alapján az eredményül kapott sűrűségfüggvény változik. Ha nem szerepel kernelparaméter, akkor a Gaussian Kernel alapértelmezés szerint meghívásra kerül. A KDE a valószínűségi sűrűségfüggvény fogalmát használja, amely segít megtalálni az adatok eloszlásának helyi maximumát. Az algoritmus úgy működik, hogy az adatpontokat vonzza egymáshoz, lehetővé téve az adatpontokat a nagy sűrűségű terület felé.
- Azok a pontok, amelyek megpróbálnak konvergálni a helyi maximumokhoz, ugyanabba a fürtcsoportba tartoznak. A K-Means klaszterezési algoritmussal ellentétben az Mean Shift algoritmus kimenete nem függ az adatpont alakjára és a klaszterek számára vonatkozó feltételezésektől. A klaszterek számát az algoritmus határozza meg az adatok vonatkozásában.
- Az Mean Shift algoritmus megvalósításának céljából az SKlearn python csomagot használjuk.
Az átlagos eltolási algoritmus megvalósítása
Az alábbiakban bemutatjuk az algoritmus megvalósítását:
1. példa
A Sklearn oktatóanyaga alapján az átlagos váltás klaszterezési algoritmusához. Az első részlet egy átmeneti algoritmust valósít meg a 2-dimenziós adatkészlet klasztereinek megtalálására. Az átlagos eltolási algoritmus megvalósításához használt csomagok.
Kód:
fromcluster importMeanShift, estimate_bandwidth
from sklearn.datasets.samples_generator import make_blobs as mb
importpyplot as plt
fromitertools import cycle as cy
Az egyik legfontosabb dolog, amit meg kell jegyeznünk, hogy a sklearn make_blobs könyvtárát használjuk az adatpontok generálására, amelyek 3 helyre összpontosulnak. Annak érdekében, hogy az átlagos eltolási algoritmust alkalmazzuk a generált pontokra, be kell állítanunk a sávszélességet, amely a hossz közötti kölcsönhatást képviseli. A Sklearn könyvtárának beépített funkciói vannak a sávszélesség becslésére.
Kód:
#Sample data points
cen = ((1, .75), (-.75, -1), (1, -1)) x_train, _ = mb(n_samples=10000, centers= cen, cluster_std=0.6)
# Bandwidth estimation using in-built function
est_bandwidth = estimate_bandwidth(x_train, quantile=.1,
n_samples=500)
mean_shift = MeanShift(bandwidth= est_bandwidth, bin_seeding=True)
fit(x_train)
ms_labels = mean_shift.labels_
c_centers = ms_labels.cluster_centers_
n_clusters_ = ms_labels.max()+1
# Plot result
figure(1)
clf()
colors = cy('bgrcmykbgrcmykbgrcmykbgrcmyk')
fori, each inzip(range(n_clusters_), colors):
my_members = labels == i
cluster_center = c_centers(k) plot(x_train(my_members, 0), x_train(my_members, 1), each + '.')
plot(cluster_center(0), cluster_center(1),
'o', markerfacecolor=each,
markeredgecolor='k', markersize=14)
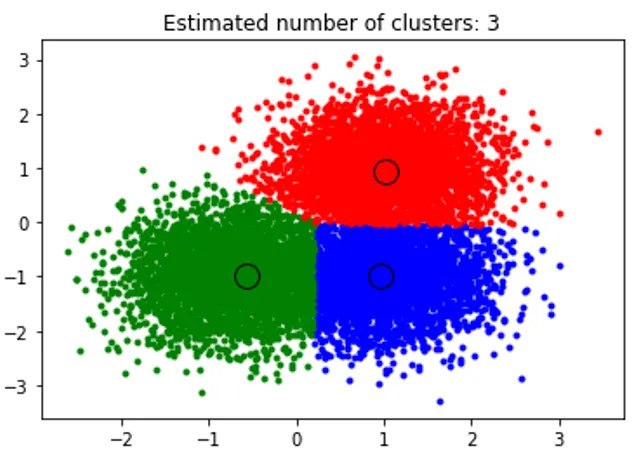
title('Estimated cluster numbers: %d'% n_clusters_)
show()
A fenti kódrészlet csoportosítást hajt végre, és az algoritmus által talált klaszterek az általunk létrehozott minden blobra összpontosulnak. Láthatjuk, hogy az alábbiakban a kivonat által ábrázolt kép mutatja az átlagos eltolási algoritmust, amely képes azonosítani a futtatás során szükséges klaszterek számát és kiszámolni a megfelelő sávszélességet az interakció hosszának ábrázolására.
Kimenet:
2. példa
A képszegmentáció alapján a számítógépes látásban. A második kivonat megvizsgálja, hogy az átmeneti algoritmus miként használt a mély tanulásban a színes kép szegmentálását. A térbeli klaszterek azonosításához az átlagos eltolás algoritmust használjuk. A korábbi kódrészletben kétdimenziós adatkészletet használtunk, míg ebben a példában a háromdimenziós helyet fogja feltárni. A kép pixelét adatpontokként kezeljük (r, g, b). A képet tömb formátumba kell konvertálnunk úgy, hogy minden pixel képviselje az adatpontot a képben, amelyet a szegmensbe megyünk. A színértékek térbe történő csoportosítása klasztersorozatokat ad vissza, ahol a fürt pixelei hasonlóak lesznek az RGB-területtel. Az átlagos eltolási algoritmus megvalósításához használt csomagok:
Kód:
importnumpy as np
fromcluster importMeanShift, estimate_bandwidth
fromdatasets.samples_generator importmake_blobs
importpyplot as plt
fromitertools import cycle
fromPIL import Image
A Snippet alatt az eredeti kép szegmentálása:
#Segmentation of Color Image
img = Image.open('Sample.jpg.webp')
img = np.array(img)
#Need to convert image into feature array based
flatten_img=np.reshape(img, (-1, 3))
#bandwidth estimation
est_bandwidth = estimate_bandwidth(flatten_img,
quantile=.2, n_samples=500)
mean_shift = MeanShift(est_bandwidth, bin_seeding=True)
fit(flatten_img)
labels= mean_shift.labels_
# Plot image vs segmented image
figure(2)
subplot(1, 1, 1)
imshow(img)
axis('off')
subplot(1, 1, 2)
imshow(np.reshape(labels, (854, 1224)))
axis('off')
A létrehozott kép kijelenti, hogy ez a megközelítés a képek alakjának azonosításához és a térbeli klaszterek meghatározásához hatékonyan végrehajtható képfeldolgozás nélkül.
Kimenet:


Előnyök és alkalmazások - az átváltási algoritmus
Az alábbiakban bemutatjuk az átlag algoritmus előnyeit és alkalmazását:
- Széles körben használják a számítógépes látás megoldására, ahol a kép szegmentálására használják.
- Az adatpontok csoportosítása valós időben, a klaszterek számának megemlítése nélkül.
- Jól teljesíti a kép szegmentálását és a videókövetést.
- Robusztusabb a szélsőségekhez képest.
Az átlagváltozás algoritmusának előnyei
Az alábbiakban felsoroljuk a pros átlag eltolás algoritmust:
- Az algoritmus kimenete független az inicializálástól.
- Az eljárás hatékony, mivel csak egy paraméterrel rendelkezik - Sávszélesség.
- Nincs feltételezés az adatcsoportok számáról és alakjáról.
- Jobb teljesítményt nyújt, mint a K-Means Clustering.
Az átlagos eltolás algoritmus hátrányai
Az alábbiakban az átmeneti algoritmus hátrányai vannak:
- Drága nagy funkciókhoz.
- A K-eszközökkel összehasonlítva nagyon lassú.
- Az algoritmus kimenete a paraméter sávszélességétől függ.
- A kimenet az ablak méretétől függ.
Következtetés
Bár ez egy egyértelmű megközelítés, amelyet elsősorban a képszegmentálással, klaszterezéssel kapcsolatos problémák megoldására használtak. Ez viszonylag lassabb, mint a K-Means, és számítási szempontból drága.
Ajánlott cikkek
Ez egy útmutató az átlagos eltolási algoritmushoz. Itt tárgyaljuk a kép szegmentálással, fürtözésével, előnyeivel és a két kernelfunkcióval kapcsolatos problémákat. Megnézheti más kapcsolódó cikkeinket, hogy többet megtudjon-
- K - klaszterezési algoritmus
- KNN algoritmus R
- Mi a genetikai algoritmus?
- Kernel módszerek
- Kernel módszerek a gépi tanulásban
- A C ++ algoritmus részletesebb magyarázata