Bevezetés a C ++ matematikai funkcióiba
Nehéz és időigényes, ha minden alkalommal kódot kell írnia, hogy elvégezze az alapvető matematikai számításokat a programban. Ezért a C ++ hatalmas számú matematikai funkciót biztosít, hogy a kód egyszerű és hatékony legyen. A matematikai függvények segítségével számos műveletet végrehajthat számokkal. Mivel ezeket a funkciókat a C ++ könyvtár beépíti és támogatja, ezért a matematikai függvények összes funkciójának használatához be kell építeni a fejlécet vagy a kód elejét. A műveletek végrehajtásához nem kell beírni a logikát kódba, ez mind a könyvtárban található.
Különböző típusú matematikai funkciók
A C ++ rengeteg különféle típusú matematikai funkciót tartalmaz, amelyeket alább említünk példákkal:
1. Maximális és minimális funkció
- max (p, q): a maximális számot adja vissza p és q között.
- min (p, q): Minimális számot ad vissza p és q között.
C ++ kód a funkcionalitás felett
#include
#include
using namespace std;
int main() (
cout << max(16, 18) << "\n";
cout << min(16, 18) << "\n";
return 0;
)
Kimenet:

2. Tápfeszültség funkciók
- pow (m, n): kiszámítja az n teljesítményre emelt m értéket.
- sqrt (m): kiszámítja m négyzetgyökét.
- cbrt (n): kiszámítja az n kockagyökét.
- hipotóp (m, n): kiszámítja a derékszögű háromszög hipotenuszát .
C ++ kód a fenti funkció megvalósításához
#include
#include
using namespace std;
int main() (
cout << pow(2, 3) << "\n";
cout << sqrt(16) << "\n";
cout << cbrt(27) << "\n";
cout << hypot(3, 4) << "\n";
return 0;
)
Kimenet:

3. Exponenciális funkciók
- exp (p): kiszámítja a p hatalomra emelt exponenciát.
- log (p): kiszámítja p p logaritmusát.
- log10 (p): kiszámítja a p általános logaritmusát.
- exp2 (p): Kiszámítja a p alap 2 exponenciáját.
- log2 (p): kiszámítja a p 2 alap logaritmusát.
- logb (p): kiszámítja p p logaritmusát.
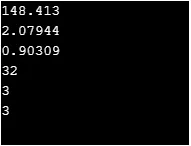
C ++ kód a fenti funkció megvalósításához
#include
#include
using namespace std;
int main() (
cout << exp(5) << "\n";
cout << log(8) << "\n";
cout << log10(8) << "\n";
cout << exp2(5) << "\n";
cout << log2(8) << "\n";
cout << logb(8) << "\n";
return 0;
)
Kimenet:
4. Egész számfunkciók
Segít megtalálni a legközelebbi egész értéket.
- ceil (z): felkerekíti z értékét.
- padló (z): lekerekíti a z értékét.
- forduló (z): lekerekíti a z értékét.
- fmod (z, y): kiszámítja a z / y osztás fennmaradó részét.
- trunc (z): A z értéket nullára kerekíti.
- rint (z): Lekerekítés móddal kerekíti a z értéket.
- nearbyint (z): Ez a kerekíti a z értéket a közeli integrális értékre.
- maradék (z, y): kiszámítja a fennmaradó z / y értéket.
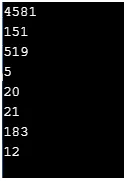
C ++ kód a fenti funkció megvalósításához
#include
#include
using namespace std;
int main() (
cout << ceil(4580.01) << "\n";
cout << floor(151.999) << "\n";
cout << round(518.5) << "\n";
cout << fmod(5, 21) << "\n";
cout << trunc(20.25) << "\n";
cout << rint(21.25) << "\n";
cout << nearbyint(182.55) << "\n";
cout << remainder(12, 36) << "\n";
return 0;
)
Kimenet:
5. Összehasonlító funkciók
A szám gyors összehasonlításban történő segítéséhez nem számít, mennyi a szám. Az alábbiakban néhány példát találunk az összehasonlító funkciókra:
- isgreater (p, q): Ellenőrzi, hogy p nagyobb-e, mint q, vagy sem.
- islessequal (p, q): Ellenőrzi, hogy p kevesebb-e vagy egyenlő-e q-val, vagy sem.
- isgreaterequal (p, q): Ellenőrzi, hogy p nagyobb-e vagy egyenlő-e q-val, vagy sem.
- islessgreater (p, q): Ellenőrzi, hogy p kisebb vagy nagyobb, mint y, vagy sem.
- nincs rendezve (p, q): Ellenőrzi, hogy p összehasonlította-e vagy sem.
C ++ kód a fenti funkció megvalósításához
#include
#include
using namespace std;
int main() (
// cout << less(22, 29) << "\n";
cout << isgreater(48, 47)<< "\n";
cout << islessequal(11, 5)<< "\n";
cout << isgreaterequal(19, 72)<< "\n";
cout << islessgreater(59, 84)<< "\n";
cout << isunordered(62, 84)<< "\n";
return 0;
)
Kimenet:

6. A trigonometrikus függvény használata
A kifejezetten geometriai számításokban használt funkciók. A derékszögű háromszög összekapcsolja a szöget a két oldal hosszának arányával.
- sin (y): kiszámítja az y szinusz értékét.
- cos (y): kiszámítja az y koszinusz értékét.
- tan (y): kiszámítja az y érintő értékét.
- asin (y): kiszámítja az inverz szinusz y értékét.
- acos (y): kiszámítja az inverz y-koszinusz értékét.
- atan (y): kiszámítja az inverz érintő y értékét.
- atan2 (y, x): kiszámítja az y és x koordináták inverz érintőjének értékét.
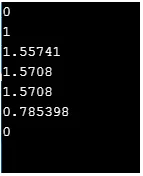
C ++ kód a fenti funkció megvalósításához
#include
#include
using namespace std;
int main() (
cout << sin(0) << "\n";
cout << cos(0) << "\n";
cout << tan(1) << "\n";
cout << asin(1)<< "\n";
cout << acos(0)<< "\n";
cout << atan(1)<< "\n";
cout << atan2(0, 1)<< "\n";
return 0;
)
Kimenet:
Íme néhány érdekes funkció, amelyek segítenek kiszámítani a hiperbolikus trigonometrikus függvények értékeit, és ezeket hiperbolikus függvényeknek nevezzük.
- sinh (x): kiszámítja az x hiperbolikus szinuszának értékét.
- cosh (x): kiszámítja az x hiperbolikus koszinusának értékét.
- tanh (x): kiszámítja az x hiperbolikus érintőjének értékét.
- asinh (x): kiszámítja az x hiperbolikus szinuszának értékét.
- acosh (x): kiszámítja az x hiperbolikus ív koszinusának értékét.
- atanh (x): kiszámítja az x hiperbolikus szinuszértékét.
C ++ kód a fenti funkció megvalósításához
#include
#include
using namespace std;
int main() (
cout << sinh(0)<< "\n";
cout << cosh(0)<< "\n";
cout << tanh(1)<< "\n";
cout << asinh(1)<< "\n";
cout << acosh(1)<< "\n";
cout << atanh(0)<< "\n";
return 0;
)
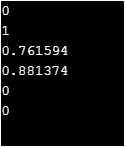
Kimenet:
Következtetés
A matematikai funkciók fontos szerepet játszanak a memória nagy mennyiségű idő- és helymegtakarításában. Az összes funkció beépített, nem kell közvetlenül végrehajtania semmilyen matematikai függvényt, csak egy fejléc fájl hozzáadásával, amely lehetőséget nyújt a matematika osztály teljes könyvtárának használatára.
Ajánlott cikkek
Ez a C ++ matematikai funkcióinak útmutatója. Itt tárgyaljuk, hogy a C ++ sokféle matematikai funkciót kínál példákkal. Megnézheti más javasolt cikkeinket -
- A C ++ felülbírálása
- Túlterhelés a C ++ kategóriában
- Négyzetgyök C ++-ban
- Tömbök C ++-ban
- Túlterhelés a Java-ban
- Négyzetgyökér a PHP-ben
- A C ++ 11 legfontosabb tulajdonságai és előnyei
- Útmutató a Négyzetgyökérhez a JavaScriptben