A lineáris regressziós modellezés áttekintése
Amikor elkezdi tanulni a gépi tanulási algoritmusokat, elkezdi tanulni az ML algoritmusok különféle módjait, azaz felügyelt, felügyelet nélküli, félig felügyelt és megerősítő tanulást. Ebben a cikkben a felügyelt tanulással és az alapvető, mégis hatékony algoritmusok egyikével foglalkozunk: Lineáris regresszió.

Ezért a felügyelt tanulás az a tanulás, amelynek során a gépet kiképezzük, hogy megértse az oktatási adatkészletben megadott bemeneti és kimeneti értékek kapcsolatát, majd ugyanazt a modellt használja a tesztelési adatkészlet kimeneti értékeinek előrejelzésére. Tehát alapvetõen, ha már van kimenete vagy címkézése a képzési adatkészletünkben, és biztosak vagyunk abban, hogy a kimenetnek van értelme a bemeneteknek megfelelõen, akkor a Felügyelt tanulást használjuk. A felügyelt tanulási algoritmusokat regresszióba és osztályozásba sorolják.
A regressziós algoritmusokat akkor használják, amikor észreveszi, hogy a kimenet folyamatos változó, míg a besorolási algoritmusokat akkor használják, amikor a kimenetet olyan részekre osztják, mint Pass / Fail, Jó / Átlagos / Rossz stb. Különböző algoritmusok vannak a regresszió vagy osztályozás végrehajtására. műveletek a Lineáris Regressziós Algoritmussal, amely a Regresszió alapvető algoritmusa.
A regresszióval szemben, mielőtt belekezdenék az algoritmusba, hadd állítsam meg az alapot az ön számára. Az iskolában remélem, hogy emlékszel a vonal egyenlet koncepciójára. Hadd mondjak röviden. Két pontot kapott az XY síkon, azaz mondjuk (x1, y1) és (x2, y2), ahol y1 az x1 kimenete és y2 az x2 kimenete, akkor a pontokon áthaladó egyenes egyenlet (y- y1) = m (x-x1), ahol m a vonal meredeksége. Most, miután megtalálta a vonal-egyenletet, ha kap egy pontmondatot (x3, y3), akkor könnyen megjósolni tudja, ha a pont a vonalon fekszik, vagy a pont távolsága a vonaltól. Ez volt az alapvető regresszió, amelyet az iskolában végeztem anélkül, hogy észrevettem volna, hogy ennek ilyen nagy jelentősége lesz a gépi tanulásban. Amit általában ebben teszünk, próbáljuk meg azonosítani azt az egyenletvonalat vagy -görbét, amely megfelelően illeszkedhet a vonat-adatkészlet bemenetéhez és kimenetéhez, majd ugyanezt az egyenletet használjuk a teszt-adatkészlet kimeneti értékének becslésére. Ez folyamatos kívánt értéket eredményez.
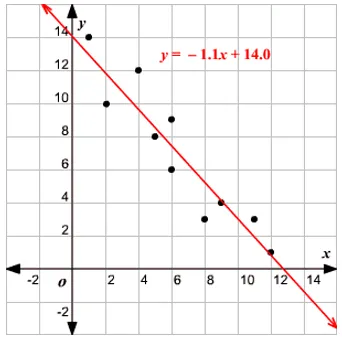
A lineáris regresszió meghatározása
A lineáris regresszió valójában nagyon hosszú ideje fennáll (mintegy 200 év). Ez egy lineáris modell, azaz lineáris kapcsolatot feltételez a bemeneti változók (x) és az egyetlen kimeneti változó (y) között. Az y értéket a bemeneti változók lineáris kombinációjával kell kiszámítani.
Kétféle lineáris regresszió van
Egyszerű lineáris regresszió
Ha egyetlen bemeneti változó van, azaz a egyenlet c
y = mx + c-nek tekintve, akkor ez az egyszerű lineáris regresszió.
Többszörös lineáris regresszió
Ha több bemeneti változó létezik, azaz a vonal egyenletet y = ax 1 + bx 2 +… nx n -nek tekintik , akkor a többszörös lineáris regresszió. Különböző technikákat alkalmaznak a regressziós egyenlet elkészítésére vagy az adatokból való kiképzésére, és a legelterjedtebb módszert ezek közönséges legkisebb négyzeteknek hívják. Az említett módszerrel készített modellt rendes legkisebb négyzetek lineáris regressziójának vagy egyszerűen legkevesebb négyzetek regressziójának nevezik. A modell akkor használatos, ha a bemeneti és a meghatározandó kimeneti értékek numerikus értékek. Ha csak egy bemenet és egy kimenet van, akkor a képződött egyenlet egy egyenlet, azaz
y = B0x+B1
ahol a vonal együtthatóit statisztikai módszerekkel kell meghatározni.
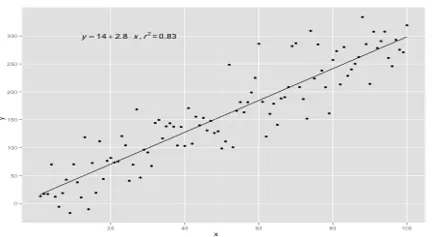
Az egyszerű lineáris regressziós modellek nagyon ritkák az ML-ben, mivel általában különféle bemeneti tényezőkkel kell meghatároznunk az eredményt. Ha több bemeneti érték és egy kimeneti érték van, akkor a képződött egyenlet egy sík vagy hipersík egyenlete.
y = ax 1 +bx 2 +…nx n
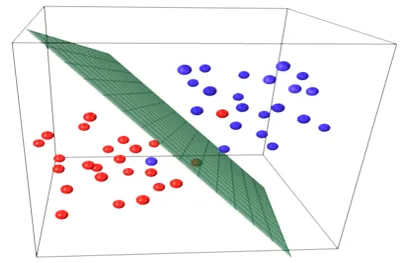
A regressziós modell alapgondolata az, hogy az adatokhoz legjobban illeszkedő vonal-egyenletet kapjunk. A legmegfelelőbb vonal az a sor, ahol a lehető legkisebbnek tartott összes adatpont esetében a teljes predikciós hiba. A hiba a sík pontja és a regressziós vonal közötti távolság.
Példa
Kezdjük egy egyszerű lineáris regresszió példájával.

A személy magassága és súlya közötti kapcsolat közvetlenül arányos. Az önkénteseken vizsgálatot végeztek a személy magasságának és ideális súlyának, valamint az értékek rögzítésének meghatározására. Ezt az edzési adatkészletünknek tekintjük. Az edzési adatok felhasználásával kiszámítják a regressziós egyenletet, amely minimális hibát eredményez. Ezt a lineáris egyenletet azután új adatokra vonatkozó előrejelzések készítésére használják. Vagyis ha megadjuk a személy magasságát, akkor a megfelelő súlyt meg kell becsülnünk az általunk kifejlesztett modell segítségével, minimális vagy nulla hibával.
Y(pred) = b0 + b1*x
A b0 és b1 értékeket úgy kell megválasztani, hogy azok minimalizálják a hibát. Ha a négyzet hibájának összegét metrikának tekintik a modell értékeléséhez, akkor a cél a vonal elérése, amely a hibát leginkább csökkenti.
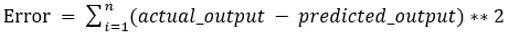
Kihúzzuk a hibát, hogy a pozitív és a negatív értékek ne töröljék egymást. Egy előrejelzővel rendelkező modell esetén:
A lehallgatás (b0) kiszámítása a vonal egyenletben az alábbiak szerint történik:
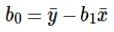
Az x bemeneti érték koefficienst kiszámítja:
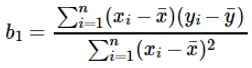
A b 1 együttható megértése:
- Ha b 1 > 0, akkor x (bemenet) és y (kimenet) közvetlenül arányosak. Ez azt jelenti, hogy az x növekedése növeli y-t, például növekszik a magasság, növekszik a súly.
- Ha b 1 <0, akkor x (prediktor) és y (cél) fordítva arányos. Ez azt jelenti, hogy az x növekedése y csökken, például a jármű sebessége növekszik, az idő csökken.
A b 0 együttható megértése:
- B 0 felveszi a modell maradványértékét, és biztosítja, hogy az előrejelzés ne legyen elfogult. Ha nem rendelkezünk B 0 kifejezéssel, akkor a (y = B 1 x) egyenlet kénytelen átmenni az origón, azaz a modellbe bevitt bemeneti és kimeneti értékek nullát eredményeznek. Ez azonban soha nem lesz akkor, ha 0 bemeneten belül, akkor B 0 az összes előrejelzett érték átlaga, ha x = 0. Ha az összes prediktív értéket 0-ra állítja x = 0 esetén, adatvesztést okoz, és ez gyakran lehetetlen.
A fent említett együtthatók mellett ez a modell normál egyenletekkel is kiszámítható. A normál egyenletek használatát és az egyszerű / multilineáris regressziós modell megtervezését a következő cikkben tovább tárgyalom.
Ajánlott cikkek
Ez egy útmutató a lineáris regressziós modellezéshez. Itt tárgyaljuk a Lineáris regresszió meghatározását, típusait, amely magában foglalja az egyszerű és a többszörös lineáris regressziót, néhány példával együtt. A következő cikkeket is megnézheti további információkért -
- Lineáris regresszió R-ben
- Lineáris regresszió az Excelben
- Prediktív modellezés
- Hogyan hozhatunk létre GLM-et R-ben?
- A lineáris regresszió és a logisztikus regresszió összehasonlítása