Bevezetés a halomfajtába C
A rendezés olyan technika, amelynek lényege az elemek különböző tulajdonságok alapján történő rendezése. (Olyan tulajdonságok, mint az adatok növekvő, csökkenő vagy ábécé sorrendben történő rendezése). Az egyik legfontosabb példa a válogatásra, amelyre itt gondolhatunk, a cikkek rendelése az online vásárlás során. Összekapcsolhatjuk az árakat, a népszerűséget, a legújabb és így tovább. Tehát számos módszer létezik az elemek pozicionálására rendezés útján. Ebben a témában a Heap Sort C-ben fogunk tanulni.
Itt a C programozási nyelven tanuljuk meg az egyik leggyakoribb rendezési technikát, a Heap Sort-t.
A Heap Sort logikája
Hogyan valósíthatjuk meg a halom válogatást? Nézzük meg alább.
Először is, a halom az egyik faalapú adatszerkezet. Az itt szereplő fa mindig egy teljes bináris fa. És kétféle halom létezik
- Min - halom: Általában növekvő sorrendben van elrendezve, vagyis ha a szülő csomópont elem értéke kisebb, mint a gyermek csomópont elem értéke.
- Max - halom: Általában csökkenő sorrendben van elrendezve, vagyis ha a szülő csomópont elem értéke nagyobb, mint a gyermek csomópont elem értéke.
Lépések a halom rendezéséhez
- Miután meg nem szerezték a válogatott listaadatokat, az elemeket a halom adatszerkezetben rendezik, akár minimális, akár max.
- A fenti lista első elemét hozzáadjuk tömbünkhöz
- A fejadat-szerkezet-technika újból kialakítását követi az első lépéssel megegyező módon, és ismét a legmagasabb vagy a legkevesebb elem kerül felvételre és hozzáadásra a tömbünkbe.
- Az ismételt lépések segítenek abban, hogy elkészítsük a tömböt a rendezett listával.
Program a halom rendezéséhez C-ben
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Először azt kérjük a felhasználótól, hogy adja meg a rendezéshez szükséges elemek számát, majd engedje meg a felhasználónak, hogy különféle elemeket írjon be, amelyeket el kell rendezni.
Követett lépések
- A következőre összpontosítunk egy halom tömb létrehozása, ebben az esetben max-halom tömb.
- A maximális halom tömb megszerzésének fő feltétele, hogy ellenőrizze, hogy a szülőcsomópont értéke nem alacsonyabb-e a gyermekcsomópont értékén. Megyünk cserélni, amíg el nem érjük ezt a feltételt.
- A teljes bináris fa fő előnye, hogy a szülő csomópont bal és jobb oldali csomópontjai 2 (i) + 1 és 2 * (i) + 2 értékekkel érhetők el. Ahol i a szülő csomópont.
- Tehát ezen a módon erre a gyökércsomóra, amely a maximális értéket tartalmazza, a jobb oldali levélcsomópont helyére kerülünk. És aztán ismét ugyanazt az eljárást követve, úgy, hogy a következő maximális szám a gyökér csomóponttá válik.
- Ugyanezt az eljárást fogjuk folytatni, amíg csak egy csomópont marad a halom tömbben.
- És aztán úgy rendezzük el a halom tömbünket, hogy egy tökéletesen rendezett tömb legyen egyre növekvő sorrendben.
- Végül kinyomtatjuk a rendezett tömböt a kimeneten.
Kimenet:
A kimenet az alábbiakban található.
Hadd mutassam meg a rendezvények képi ábrázolását:
- A bevitt adatokat először egydimenziós tömb formájában ábrázoljuk, az alábbiak szerint.

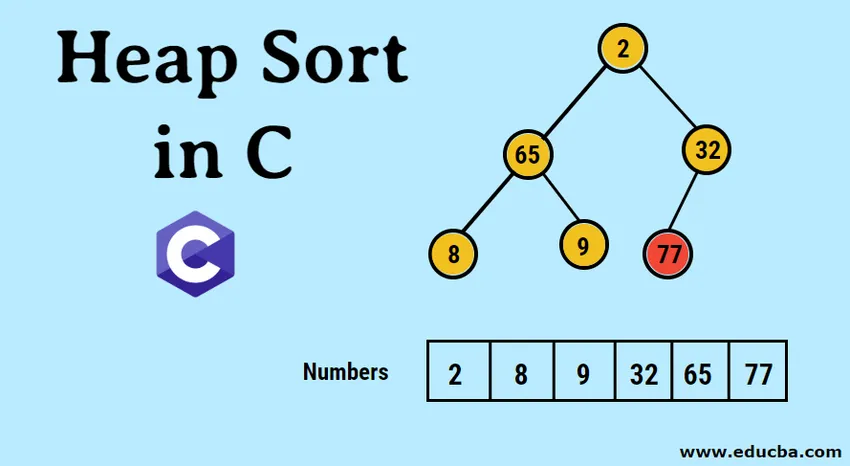
- A képződött bináris fa képi ábrázolása a következő:
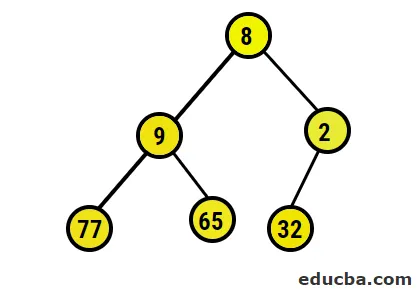
- Most átváltunk a maximális halomra, ügyelve arra, hogy minden szülőcsomó mindig nagyobb legyen, mint a gyermekcsomópontok. Amint azt a kimeneten halom szerinti rendezett tömb alatt említik, a képi ábrázolás a következő lenne:
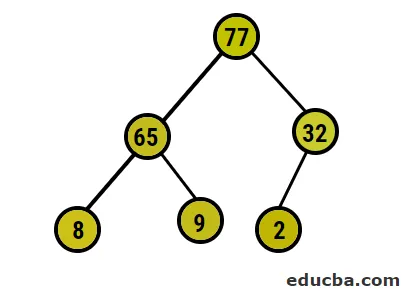
- Ezután cseréljük ki a gyökércsomót a szélső levélcsomópontra, majd töröljük a fáról. A levélcsomó lenne a gyökér most és újra ugyanazt az e folyamatot követve, hogy megkapja a legmagasabb elemet a gyökérben
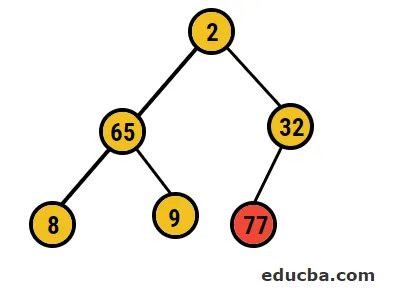
- Tehát ebben az esetben 77 számjegyet törölnek ebből a fából, és behelyezik a rendezett tömbbe, és a folyamat megismétlődik.
A fentiekben láthattuk max. Halom tömb létrehozására. Ugyanezt az eljárást kell kezelni a min-halom tömb kialakításával is. Mint fentebb tárgyaltuk, az egyetlen különbség a szülő és a gyermek csomópont elemei közötti kapcsolat.
Gyakorlatként megpróbálhatja csökkenő sorrendben kialakítani a halom fajtáját?
Következtetés
Noha sok válogatási technika létezik, a halom válogatást idő és tér bonyolultsága miatt az egyik jobb válogatási módszernek tekintik. A legjobb, az átlagos és a legrosszabb eset időbeli összetettsége O (nlogn), ahol a legrosszabb eset komplexitása jobb, mint a Quicksort legrosszabb esetének komplexitása, és a tér komplexitása O (1).
Ajánlott cikkek
Ez egy útmutató a Heap Sort in C-hez. Itt tárgyaljuk a Heap Sort logikáját és lépéseit a mintakóddal és a kimenettel, valamint a képi ábrázolásokkal. Lehet, hogy megnézi a következő cikkeket is, ha többet szeretne megtudni -
- Heap Sort in Java
- Kiválasztás Rendezés Java-ban
- Palindrome a C programban
- Minta a C programozásban
- Halom sorrendje C ++-ban (algoritmus)
- Halom Rendezés Pythonban
- C Programozó mátrix szorzás