
Meghatározási együttható képlet (Tartalomjegyzék)
- Képlet
- Példák
Mi a meghatározási együttható képlete?
A statisztikákban a meghatározási együttható, amelyet R2-nek is neveznek, olyan eszköz, amely meghatározza és felméri a statisztikai modell azon képességét, hogy megmagyarázza és előrejelezze a jövőbeli eredményeket. Más szavakkal, ha van egy függő y változó és független x változó egy modellben, akkor R2 segít meghatározni az y variációt az x variációval. Ez a regressziós elemzés egyik legfontosabb eredménye, és akkor használják, amikor előre jelezzük a jövőt, vagy tesztelünk néhány modellt kapcsolódó információkkal. Az R2 értéke 0 és 1 között van, és annál magasabb az R2 értéke, annál jobb lesz a modell előrejelzése és erőssége. Az R 2 nagyon hasonló a korrelációs együtthatóhoz, mivel a korrelációs együttható két változó közvetlen társulását méri. R2 alapvetően egy korrelációs együttható négyzete.
A meghatározási együttható képlete:
A meghatározási együttható kiszámításához több képlet létezik:
- Korrelációs együttható használata:
Correlation Coefficient = Σ ((X – X m ) * (Y – Y m )) / √ (Σ (X – X m ) 2 * Σ (Y – Y m ) 2 )
Hol:
- X - Adatpontok az X adatkészletben
- Y - adatpontok az Y adatkészletben
- X m - az X adatkészlet átlaga
- Y m - az Y adatkészlet átlaga
Így
Coefficient of Determination(R 2 ) = (Correlation Coefficient) 2
- Regressziós kimenetek használata
Meghatározási együttható (R 2 ) = Magyarázott variáció / Teljes variáció
Meghatározási együttható (R 2 ) = MSS / TSS
Coefficient of Determination (R 2 ) = (TSS – RSS) / TSS
Hol:
- TSS - a négyzetek teljes összege = Σ (Yi - Ym) 2
- MSS - A négyzetek modellösszeg = Σ (Y - Ym) 2
- RSS - négyzetek maradékösszege = Σ (Yi - Y ^) 2
Y a modell becsült értéke, Yi az i. Érték és Ym az átlagérték
Példák a meghatározási együttható képletére (Excel sablonnal)
Vegyünk egy példát a meghatározási együttható kiszámításának jobb megértésére.
Itt töltheti le a meghatározási együtthatót tartalmazó képlet Excel sablonját - a meghatározási együtthatót képlet Excel sablonnal.A meghatározási együttható képlete - 1. példa
Tegyük fel, hogy két X és Y adatkészlettel rendelkezik, és mindegyik 20 véletlenszerű adatpontot tartalmaz. Számítsa ki a meghatározási együtthatót az X és Y adatkészletre.
Az átlag kiszámítása:
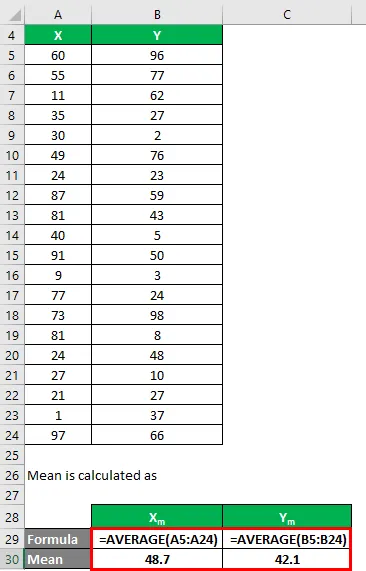
- Az X adatkészlet átlaga = 48, 7
- Az Y = 42, 1 adatkészlet átlaga
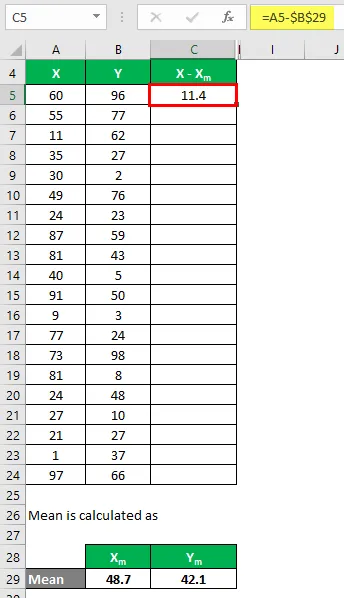
Most ki kell számolnunk az adatpontok és az átlagérték közötti különbséget.
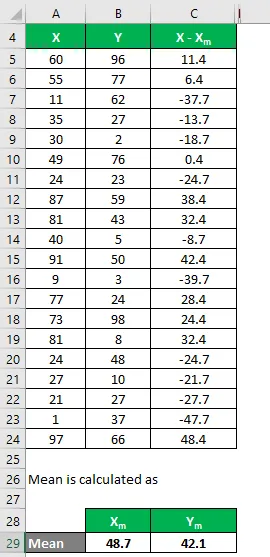
Hasonlóképpen számítsa ki az összes X adatkészletre.
Hasonlóképpen számítsa ki az Y adatkészletre is.

Számítsa ki a különbség négyzetét mind az X, mind az Y adatkészletre.
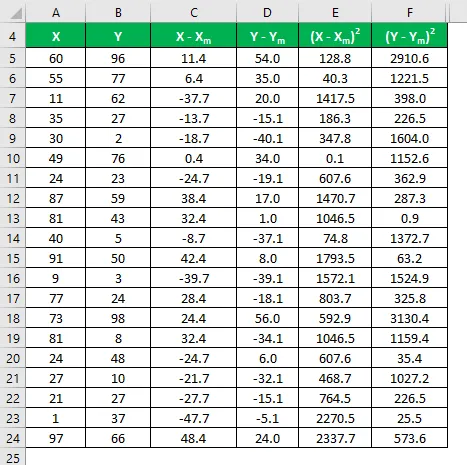
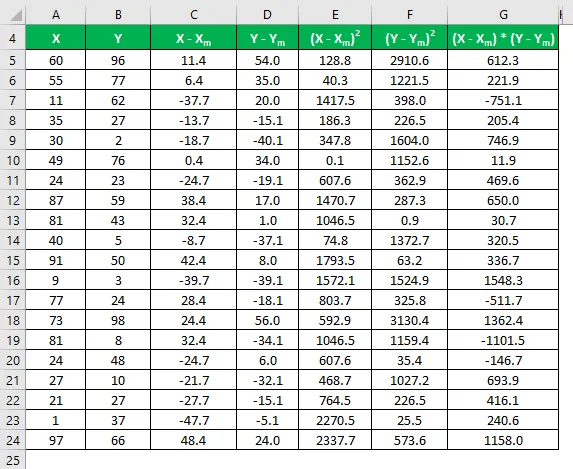
Szorozzuk meg a különbséget X-ben Y-vel.
A korrelációs együtthatót az alábbiakban megadott képlettel kell kiszámítani
Korrelációs együttható = Σ ((X - X m ) * (Y - Y m )) / √ (Σ (X - X m ) 2 * Σ (Y - Y m ) 2 )
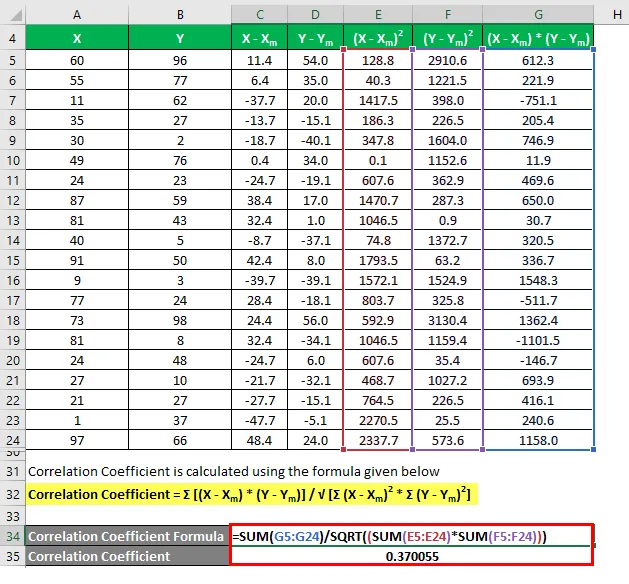
A meghatározási együtthatót az alábbiakban megadott képlettel kell kiszámítani
Meghatározási együttható = (korrelációs együttható) 2
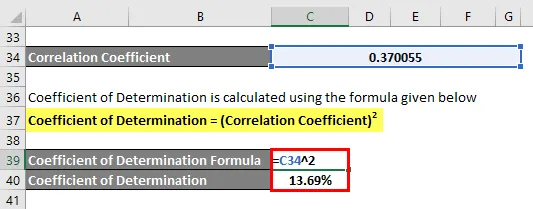
Meghatározási együttható = 13, 69%
A meghatározási együttható képlete - 2. példa
Tegyük fel, hogy nagyon kockázatkerülő befektető, és pénzt szeretne befektetni a tőzsdére. Nem biztos abban, hogy melyik részvénybe fektetne be, és alacsony a kockázatvállalási hajlandósága is. Ezért biztonságos részvényt szeretne befektetni, amely utánozza az index teljesítményét. Barátja, aki aktív befektető, 3 részvényt választott neked az alapvető és technikai információk alapján, és azt szeretné, hogy e részek közül 2-et válasszon.
Információkat gyűjtött az utóbbi 15 év történelmi visszatéréséről is.
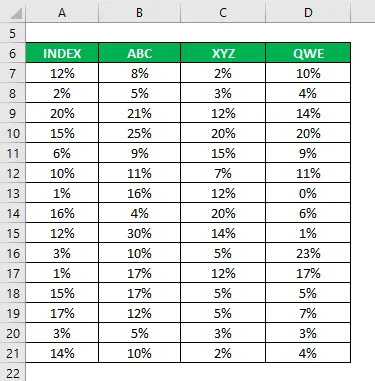
A korrelációs együtthatót az Excel képlettel számolják
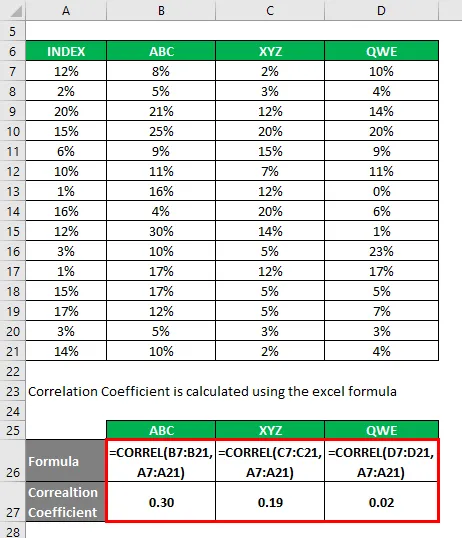
A meghatározási együtthatót az alábbiakban megadott képlettel kell kiszámítani
Meghatározási együttható = (korrelációs együttható) 2
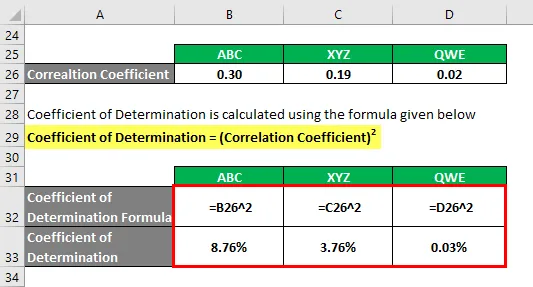
Az információk alapján kiválasztja az ABC és az XYZ részvényt, amelyet befektetni kívánnak, mivel ezek a legnagyobb meghatározási együtthatóval rendelkeznek.
Magyarázat
A fentiekben ismertetett meghatározási együttható a két adatkészlet közötti korreláció négyzete. Ha R2 0, ez azt jelenti, hogy nincs korreláció, és a független változó nem tudja megjósolni a függő változó értékét. Hasonlóképpen, ha értéke 1, ez azt jelenti, hogy a független változó mindig sikeresen megjósolja a függő változót. Vannak azonban bizonyos korlátok is. Annak ellenére, hogy megmondja nekünk a 2 adatkészlet közötti korrelációt, nem azt mondja meg, hogy elegendő-e ez az érték vagy sem.
Ezenkívül a nagy R 2 érték nem mindig azt jelenti, hogy a 2 változónak szoros kapcsolata van, és ez is fluke lehet. Például: Tegyük fel, hogy az év során eladott autók száma és az évente eladott fagylalt dobozok közötti R2 érték 80%. De ezek között nincs kapcsolat. Tehát nagyon óvatosnak kell lennie az R2 használata során, először meg kell értenie az adatokat, majd alkalmaznia kell a módszert
A meghatározási együttható képletének relevanciája és felhasználása
Az R2 sok gyakorlati alkalmazására van lehetőség. Például az R2-t nagyon gyakran használják a befektetők, hogy összehasonlítsák portfóliójának teljesítményét a piaccal, és megpróbálják megjósolni a jövőbeli irányokat is. Hasonlóképpen, a fedezeti alapok az R 2 felhasználásával segítik őket a kockázatok modellezésében. De végül az eredmény tiszta számokon és statisztikákon alapul, amelyek időnként félrevezetőek lehetnek. Mint fentebb említettem, először ellenőriznünk kell, hogy az R2 kimenetének van-e értelme a valós életben, vagy sem.
Ajánlott cikkek
Ez egy útmutató a meghatározási együttható képletéhez. Itt megvitatjuk, hogyan lehet kiszámítani a meghatározási együtthatót, a gyakorlati példákkal és a letölthető excel sablonnal együtt. A következő cikkeket is megnézheti további információkért -
- Útmutató a piaci kockázat prémium képletéhez
- Példák a fedezeti arány képletre
- Számológép a tevékenységalapú költségszámítási képlethez
- Hogyan lehet kiszámítani az információarányt a képlet segítségével?