
Bevezetés a szórási példákba
Rengeteg példa van a standard eltérésekre. A szórás az adatkészlet szóródásának mértéke, azaz a számok eloszlása. Hasznos, ha összehasonlítjuk azokat a különféle adatkészleteket, amelyeknek átlaga azonos, de eltérő lehet. A következő különféle standard eltérés példája megértést nyújt a leggyakoribb helyzetekről, amikor a szórást kiszámítják, és hogyan lehet ugyanazt kiszámítani
Példák a szórásra
Az alábbiakban bemutatjuk a standard eltérés példáit
Szabvány eltérés - 1. példa
A Z társaság részvényeinként 50 USD áron ad el eladást, és ugyanazokat a kifizetéseket követeli a következő évre vonatkozóan:
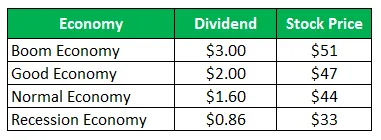
Számítsa ki a szórást, ha mind a négy forgatókönyv megadása valószínű.
Megoldás:
A tartási periódus (HPR) kiszámítása a következő:
A HPR képlete
HPR = ((periódus vége - eredeti érték) + jövedelem) / eredeti érték) * 100
A boom gazdaság számára
- HPR (gém) = ((51-50) + 3) / 50 = 8, 00%
- HPR (jó) = ((47-50) + 2) / 50 = -2, 00%
- HPR (normál) = ((44-50) + 1, 60) / 50 = -8, 80%
- HPR (recesszió) = ((33-50) + 0, 86) / 50 = -32, 28%
A várható hozam kiszámítása
Mivel az összes forgatókönyv egyformán valószínű, ezért minden valószínűsége ¼ lesz
A várható visszatérés képlete
Várható visszatérés ((Boom valószínűsége * Return of Boom) + (Jó valószínűsége * Visszatérés jóból) + (Normál valószínűsége * Visszatérés normálból) + (Recesszió valószínűsége * Visszatérés recesszióból)
- Várható hozam = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8, 80%) + (1/4 x -32, 28%)
- Várható hozam = -8, 77%
A szórás kiszámítása
A variancia képlete
Variancia = (A szórókeret fellendülésének valószínűsége * (A gém visszatérése - Teljes várt hozam) 2) + (Jó valószínűsége * (Jó hazatérés - Összes várható hozam) 2) + (Normál valószínűsége * (Normál visszatérés - Teljes várt hozam) 2 ) + (A recesszió valószínűsége * (visszatérés a recesszióból - a várható visszatérés teljes összege) 2)
- Variancia = 1/4 (8 - (-8, 77)) 2 + 1/4 (-2 - (-8, 77)) 2 + 1/4 (-8, 80 - (-8, 77)) 2 + 1/4 (-32, 28 - (-8, 77)) 2
- Variáns = 219, 95
A szórás képlete
A szórás négyzet alakú variancia
Szabványbeli eltérés = √Variance
- Szabványbeli eltérés = √ 219, 95
- Szabványbeli eltérés = 14, 83%
Példa a standard eltérésre - 2
Szabvány eltérés a portfólióban szereplő két társaság esetében
Az A társaság törzsrészvénye egy részvényenként 28 dollárért árusítja, és ugyanazok az ajánlatok kínálják a következő év kifizetéseit követően

A B társaság törzsrészvénye részvényenként 93 dollárért elad, és ugyanazokat az összegeket kínálja a következő év kifizetéseire:

a) Számolja ki az A társaság szórását
b) Számítsa ki a B. társaság szórását
c) Számítsa ki a portfólió szórását, ha a befektetés fele az A társaság, a többi fele a B. társaságban
Megoldás:
Az A társaság számára
A tartási periódus (HPR) kiszámítása
A HPR képlete
HPR = ((periódus vége - eredeti érték) + jövedelem) / eredeti érték) * 100
- HPR (gém) = ((20-28) + 1) / 28 = -25, 00%
- HPR (normál) = ((30-28) + 1, 50 / 28 = 12, 50%
- HPR (recesszió) = ((38-28) + 5) / 28 = 53, 57%
A társaság várható hozamának kiszámítása
A várható visszatérés képlete
Várható visszatérés ((a gém valószínűsége * visszatérés a gémből) + (a normál valószínűsége * visszatérés a normálból) + (a recesszió valószínűsége * visszatérés a recesszióból)
- Várható hozam = (0, 45 x -25, 00%) + (0, 35 x 12, 50%) + (0, 20 x 53, 57%)
- Várható hozam = 3, 84%
A szórásos társaság kiszámítása
A variancia képlete
Variancia = (A szórókeret fellendülésének valószínűsége * (A fellendülés szórása - teljes várt hozam) 2) + (A normál valószínűsége * (Visszatérés a normálból - A teljes várt hozam) 2 ) + (A recesszió valószínűsége * (Visszatérés a recesszióból - A teljes várt hozam) 2)
- Variancia = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Variáns = 895, 15
A szórás képlete
A szórás négyzet alakú variancia
Szabványbeli eltérés = √Variance
- Szabványbeli eltérés = √ 895, 15
- Szabványbeli eltérés = 29, 92%
A B. társaság számára
A tartási periódus (HPR) kiszámítása
A HPR képlete
HPR = ((periódus vége - eredeti érték) + jövedelem) / eredeti érték) * 100
HPR (gém) = ((200-93) +7) / 93 = 122, 58%
HPR (normál) = ((105-93) + 5, 50 / 93 = 18, 82%
HPR (recesszió) = ((4-93) +2) / 93 = -93, 55%
A várható hozam kiszámítása
A várható visszatérés képlete
Várható visszatérés ((a gém valószínűsége * visszatérés a gémből) + (a normál valószínűsége * visszatérés a normálból) + (a recesszió valószínűsége * visszatérés a recesszióból)
- Várható hozam = (0, 45x122, 58%) + (0, 35x18, 82%) + (0, 20x -93, 55%)
- Várható hozam = 43, 04%
A szórás kiszámítása
A variancia képlete
Variancia = (A szórókeret fellendülésének valószínűsége * (A fellendülés szórása - teljes várt hozam) 2) + (A normál valószínűsége * (Visszatérés a normálból - A teljes várt hozam) 2 ) + (A recesszió valószínűsége * (Visszatérés a recesszióból - A teljes várt hozam) 2)
- Variancia = 0, 45 (122, 58– (43, 04)) 2 + 0, 35 (18, 82– (43, 04)) 2 + 0, 20 (-93, 55– (43, 04)) 2
- Variáció = 6783.65
A szórás képlete
A szórás négyzet alakú variancia
Szabványbeli eltérés = √Variance
- Szabványbeli eltérés = √6783.65
- Szabványbeli eltérés = 82, 36%
Az A és a B. társaságba fektetett portfólió várható hozamának és szórásának kiszámítása
Az A társaság szórása = 29, 92%
A B társaság szórása = 82, 36%
Az A társaság súlya = 0, 50
A B társaság súlya = 0, 50
A portfólió szórásának képlete
A portfólió szórása = (az A társaság súlya * az A társaság várható hozama) + ((a B társaság súlya * a B társaság várható hozama)
- A portfólió szórása = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- A portfólió szórása = 56, 14%
Elemzés
A portfólió szórása alacsonyabb, mint bármelyik részvény esetében, mivel a készletek diverzifikáltak különböző részvényekben. A diverzifikáció a kockázat csökkentéséhez vezet, hacsak nem áll fenn tökéletes korreláció a portfólióbefektetések hozama között.
Következtetés - Példák standard eltérésre
A szórás az adathalmaz szétszóródását méri az átlaghoz viszonyítva. Ezt a variancia négyzetgyökével számolják. Minél nagyobb az értékpapír szórása, annál nagyobb az ár és az átlag közötti szórás, ami azt mutatja, hogy az ártartomány nagy. A fent említett példák a standard eltérés különböző példáinak néhány példája. Számos más példa is létezik, amelyek azt mutatják, hogy a szórást más adatokkal lehet kiszámítani.
Ajánlott cikkek
Ez egy útmutató a standard eltérési példákhoz. Itt tárgyaljuk a standard eltérés különféle példáit és részletes magyarázatát . Lehet, hogy megnézi a következő cikkeket is, ha többet szeretne megtudni -
- Rögzített költségek példa
- Változó költségszámítási példa
- Kvantitatív kutatási példa
- Monopolista versenypéldák