Excel NORMSINV - Hogyan lehet használni a NORMSINV Képletet az Excelben?

Excel NORMSINV (Tartalomjegyzék)

• Bevezetés az Excel NORMSINV-be
• Hogyan lehet használni a NORMSINV Képletet az Excelben?

Bevezetés az Excel NORMSINV-be

Az inverz normál kumulatív eloszlási függvény Excelben egy fontos eszköz, amely egy adott valószínűségértékre visszatéríti a fordított normál kumulatív eloszlást, azaz általában a normál normál kumulatív eloszlás inverzét adja vissza (amelynek nulla átlaga és standard eltérése egy). A NORM.S.INV funkciót először a Microsoft excel 2010 verziójában vezetik be, amely a NORMSINV funkció frissített verziója az Excel 2013-ban és a legújabb verzió. A NORMSINV funkciót elsősorban a követelések és a pénzügyi elemzések során használják.

Az Excel NORMSINV szintaxisa

Érv:

Valószínűség - ami csak a valószínűség, hanem a normál eloszlásnak felel meg.

Hogyan lehet használni a NORMSINV Képletet az Excelben?

A Microsoft excel programjában a NORMSINV beépített funkciót statisztikai függvénybe soroljuk, amelyet az alábbi képernyőképe mutat be (ahol kiszámítja egy adott valószínűségre a normál kumulatív eloszlás inverzét).

• Lépjen a Képletek menübe.
• Kattintson a További funkciók elemre az alábbi képernyőképen látható módon.

• Válasszon statisztikai kategóriát, amelyben megtalálja a NORM.DIST függvényt, az alább látható módon.

1. példa - A NORM.DIST és a NORMSINV használata

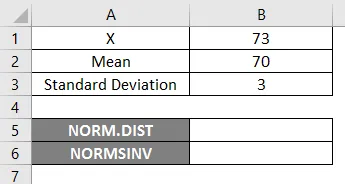
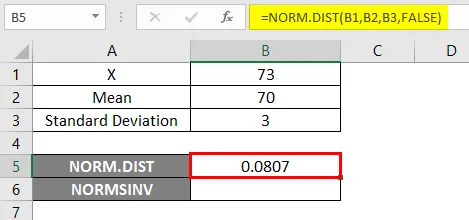
A NORM.DIST függvény használatához kezdjük egy egyszerű példával, ahol ki kell deríteni a hallgatói osztályokat. Tegyük fel, hogy az osztályvizsga átlagértéke 70, azaz mu = 70, és az osztály szórása 3 pont, azaz sigma = 3 Itt ki kell derítenünk, mi a valószínűsége annak, hogy a hallgatók a 73-as vagy annál alacsonyabb pontokat kapják, azaz P (X <= 73). Tehát lássuk, hogyan lehet megtudni a valószínűséget a NORM.DIST függvény segítségével.

• X = 3
• Átlag = 70
• Szabványbeli eltérés = 3

• Használja a NORM.DIST funkciót az alábbiak szerint.

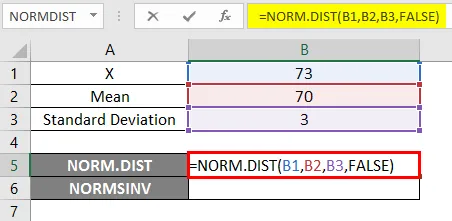
• Ha alkalmazzuk a fenti NORM.DIST függvényt, akkor a valószínűsége 0.0807.

• Most alkalmazza a NORMSINV függvényt a normál kumulatív eloszlás inverzének az alább bemutatott megértéséhez.

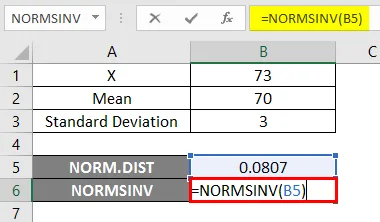
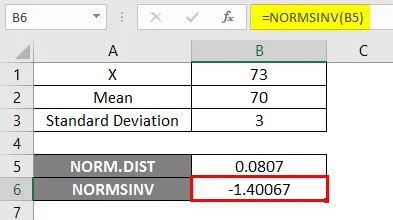
Eredmény -

Az alábbi eredményben láthatjuk, hogy az adott valószínűségre, azaz a normál kumulatív eloszlás inverzére negatív értékeket -1.40067 kapunk.

2. példa - Átlagos és pontos szórás

Lásd még egy példát görbealapú adatokkal, hogy megismerjük az átlagot és a pontos szórást.

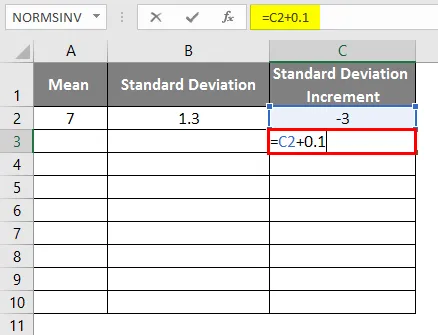
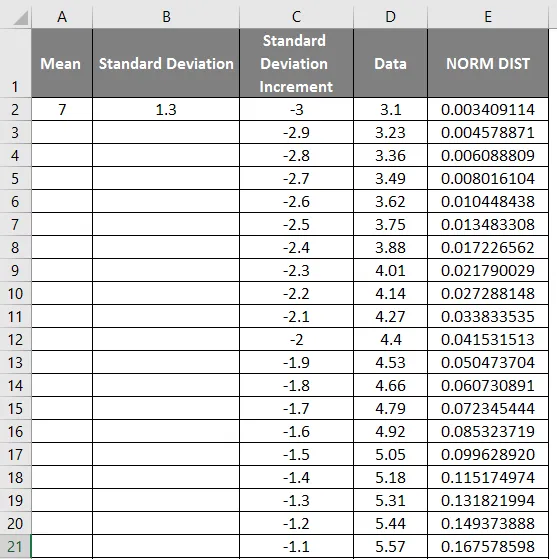
• Átlag = 7
• Szabványbeli eltérés = 1.3
• A szórás növekedése -3-ként

• A csengőgörbe eléréséhez 0, 1-et kell hozzáadnunk a szórási növekményhez, ahol az adatok az alábbiak szerint vannak feltüntetve.

• A képlet alkalmazása után az alábbi ábra mutatja az eredményt.

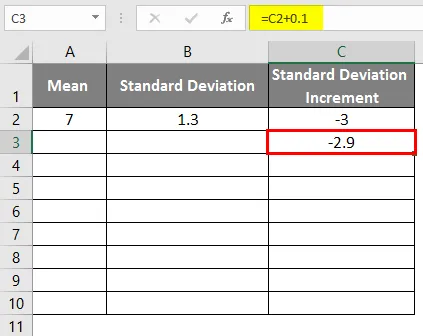
• Húzza az értékeket, hogy további értékeket kapjon, amíg meg nem kapjuk a pozitív értékeket, így bal oldali görbét kapunk.

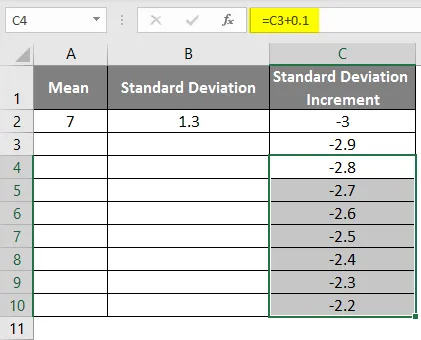
• A jobb görbe eléréséhez a következő képletet kell alkalmaznunk, mint = átlag-szórás * 3, hogy a pontos görbéket kapjuk.

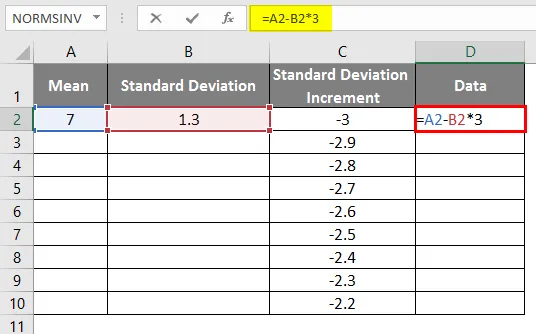
• A képlet használata után az eredmény az alábbiakban látható.

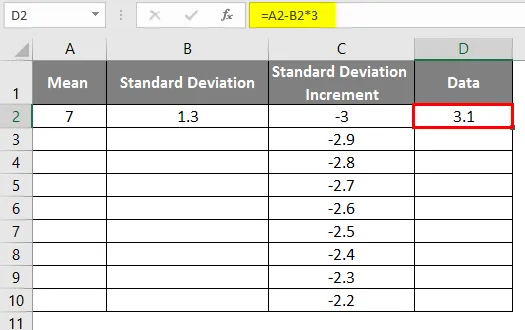
• Mint a fenti adatokban a szórás növekedésekor a bal oldali görbe eléréséhez, az értékeket 0, 1-rel növeljük
• Ugyanazt a forgatókönyvet alkalmazzuk, ha a képletet alkalmazzuk: = 3.1 + SZABVÁNYOS DEVIÁCIÓ / 10, hogy a görbe növekedése 0, 1 legyen

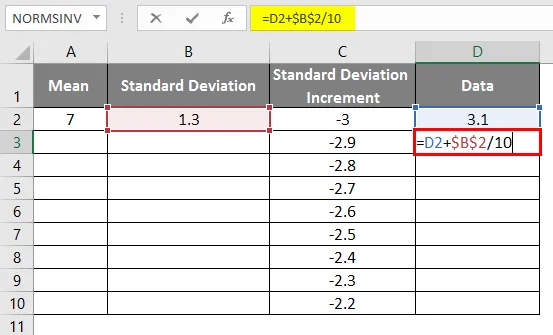
• A képlet használata után az eredmény az alábbiakban látható.

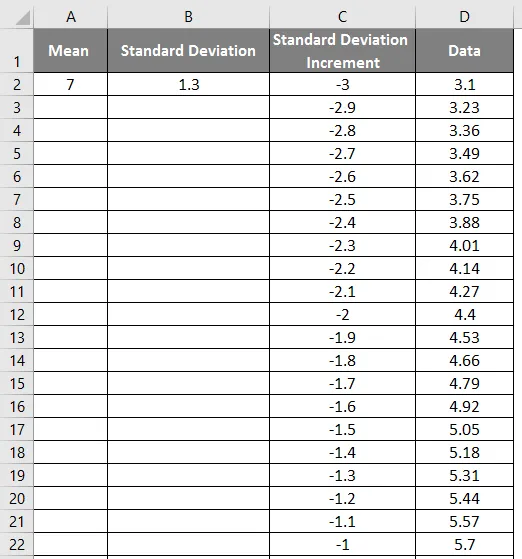
• Húzza az értékeket, hogy pontos eredményt kapjon, amely az alábbi képernyőképen látható.

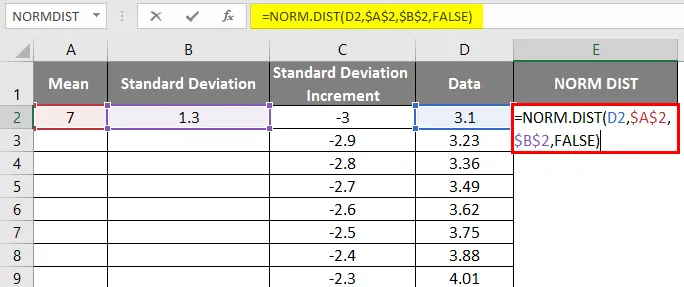
• Most alkalmazza a normál eloszlási függvényt a következő képlettel: = NORM.DIST (ADAT érték, átlag, szórás, hamis).

• Az alábbi eredményt kapjuk az alábbiak szerint.

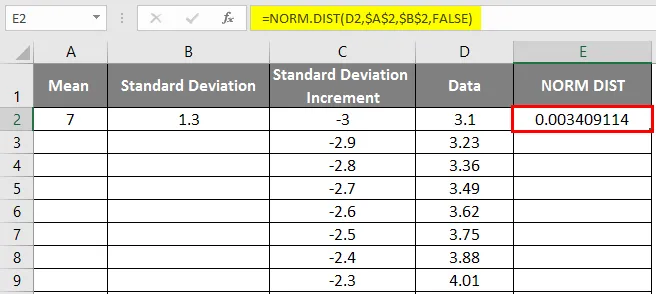
• Húzza az értékeket az alább bemutatott pontos eredmény eléréséhez.

• Amint a fenti képernyőképen látható, kiszámítottuk a NORMAL eloszlást az átlag és a szórás alapján. Most lássuk, mi lesz a NORMAL eloszlás fordítottja az alább bemutatott NORMSINV alkalmazásával.

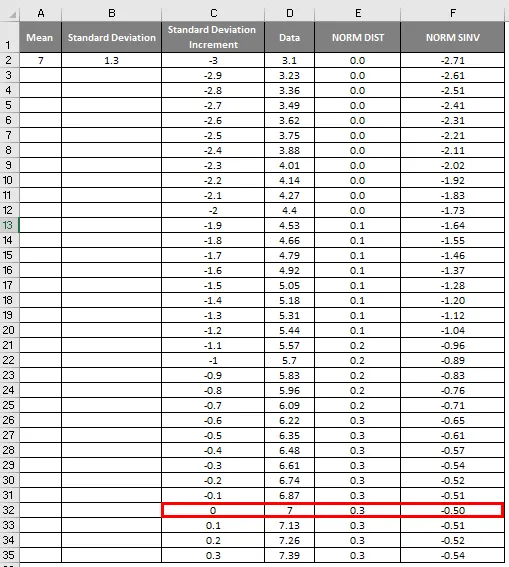
• Itt láthatjuk, hogy a Zero érték (0) szórása 7.

Szétoszlatott grafikon alkalmazásával megnézheti, hogyan jelenik meg a bal és a jobb görbe.

• Először válassza ki az adatokat és a Normál oszlopot.
• Lépjen a Beszúrás fülre, és válassza ki a szétszórt grafikát az alábbiak szerint.

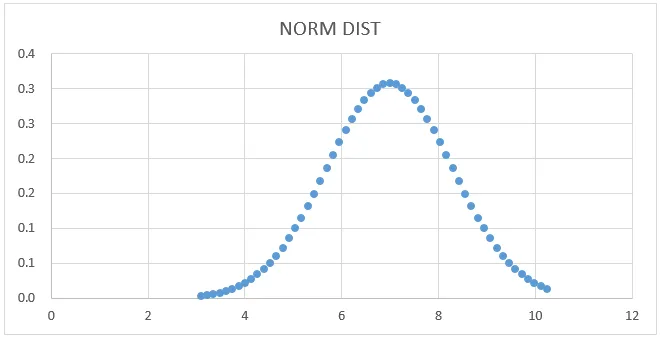
• Az alábbi görbe grafikonot kapjuk, az alább látható módon.

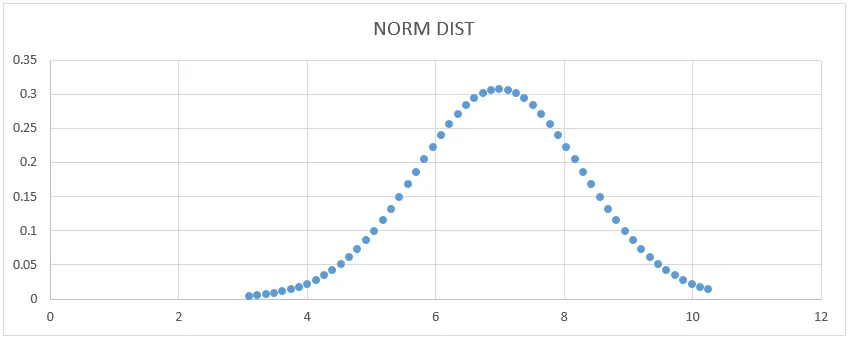
Itt láthatjuk, hogy a 7. átlagérték standard eltérés alakú, ahol ezt megmutathatjuk egy egyenes vonal ábrázolásával.

• Átlag = 7
• 1 - A szokásos eltérés az adatok 68% -át jelzi.
• 2 - A szokásos eltérés az adatok 95% -át jelzi.
• 3 - A szokásos eltérés az adatok 99, 7% -át jelzi.

Normál eloszlási grafikon:

NORMSINV grafikon:

A fenti ábrából válassza ki az adat oszlopot és a NORM SINV értéket az alábbiak szerint.

• Először válassza ki az adatokat és a Normál oszlopot.
• Lépjen a Beszúrás fülre, és válassza ki a szétszórt grafikont.
• Megkapjuk az alábbi grafikont, amely az alábbi képernyőképen látható.

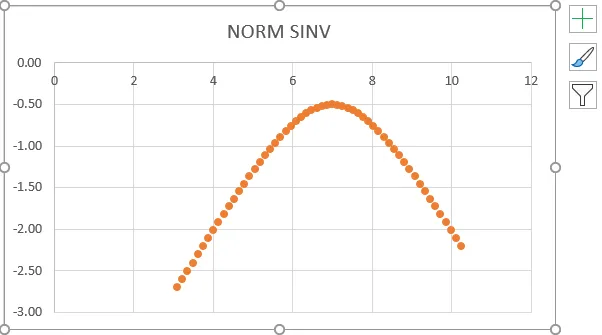
• A fenti képernyőképről láthatjuk, hogy a normál eloszlás pontos inverzét kaptuk, amely ugyanazt az ábrát mutatja.

3. példa - A bal és a jobb görbe konfigurálása

Ebben a példában a bal és a jobb görbét a normál eloszlás függvényében konfiguráljuk. Vegye figyelembe az alábbi adatokat, az alább látható módon, ahol x negatív értékei vannak, és pozitív értékre növekszik.

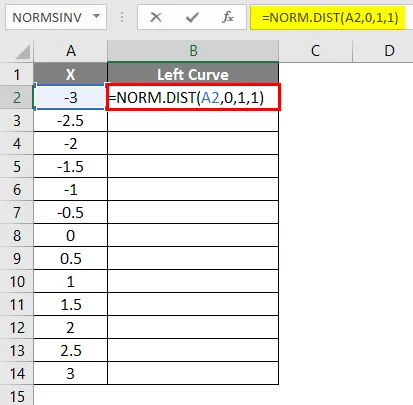
• Alkalmazza a = NORM.DIST (A2, 0, 1, 1) képletet.

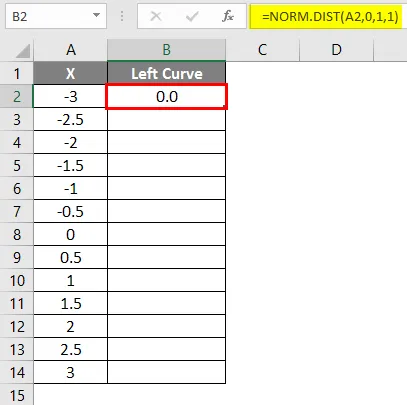
• A képlet alkalmazása után az eredmény az alábbiakban látható.

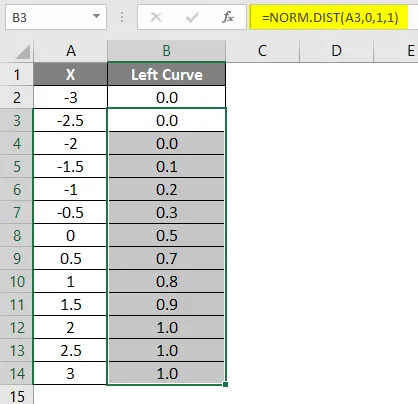
• Húzza a képletet más cellákba.

• Alkalmazza a képletet = 1-B2 .

• A képlet alkalmazása után az eredmény az alábbiakban látható.

• Húzza ugyanazt a képletet más cellákba.

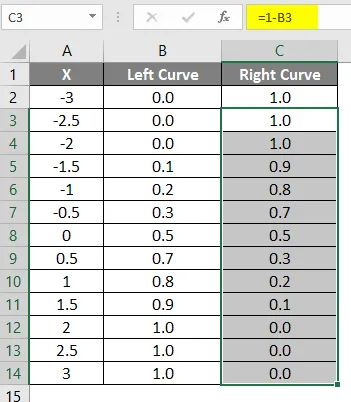
A fent alkalmazott képlet eredményét az alábbiakban mutatjuk be.

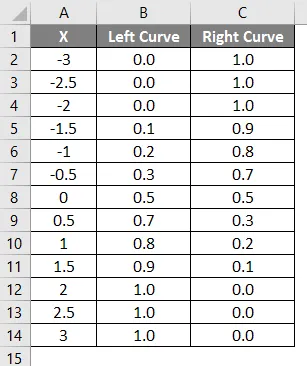
• A bal oldali görbe értékeit a NORMAL DISTRIBUTION képlet alkalmazásával számítottuk ki úgy, hogy a halmozott értéket igaznak állítottuk be, és a NORMSINV értéket a bal görbe alapján számítottuk ki.

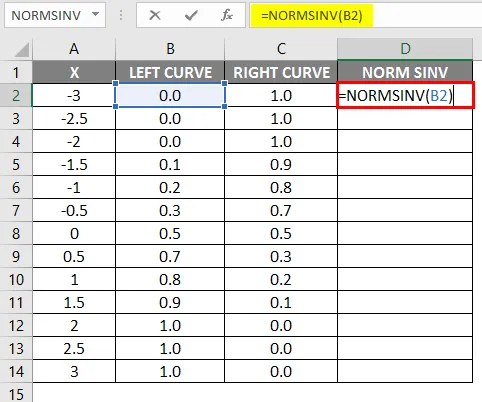
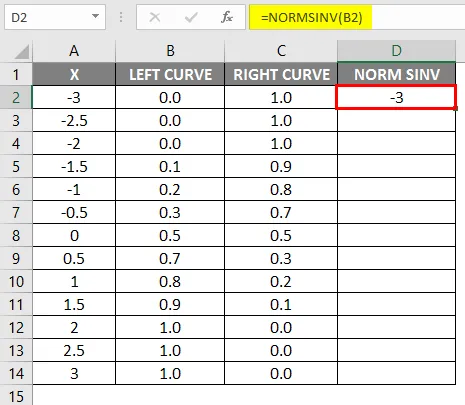
• A képlet alkalmazása után az eredmény az alábbiakban látható.

• Húzza ugyanazt a képletet más cellákba.

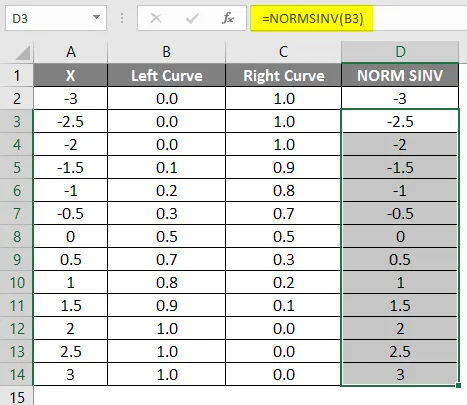
Mint láthatjuk, hogy ugyanazt az értéket kaptuk a NORMSINV-re, amely nem más, mint a normál eloszlás fordítottja. Ugyanígy kapjuk meg a megfelelő görbe értéket az 1 bal oldali görbe értékének kiszámításával. A következő lépésben ellenőrizni fogjuk, hogyan kapjuk meg az x magasságát a szétszórt gráf segítségével.

• Válassza ki a bal oldali kikeményedési és a jobb oldali görbe oszlopot.
• Lépjen a beszúrás menübe.
• Válassza ki a szétszórt grafikát az alábbiak szerint.

Az alábbi grafikon eredményt kapjuk az alább látható módon.

NORM SINV grafikon:

Az alábbi grafikonon láthatjuk, hogy a NORM DISTRIBUTION érték bal oldali görbéje pontosan megegyezik a (0, 0, 5) értékkel, amely a vonal közepén helyezkedik el, ahol ugyanazt a grafikonot kapjuk, ha a NORMDIST-re jelentkezünk.

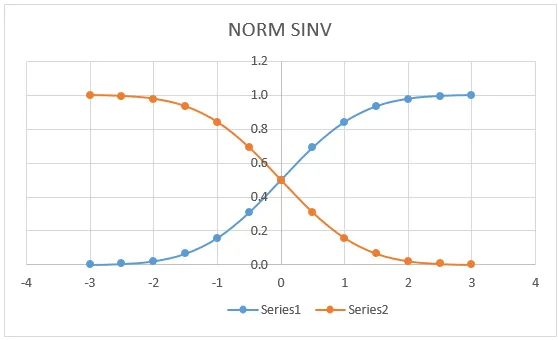
A fenti grafikonon egyértelműen megmutatkozik, hogy a pontos átlagot egy középpontban kaptuk, amely jelöli:

• X = 0
• Bal görbe = 0, 5
• Jobb görbe = 0, 5

Megjelenítettük a NORMSINV értékeket grafikus formátumban, az alább látható módon.

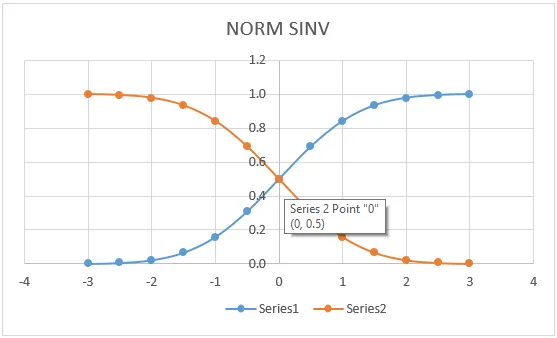
Ne feledje, mi az Excel NORMSINV

• #érték! Hiba akkor fordul elő, ha az adott argumentum nem numerikus vagy logikai érték.
• A Normal Distribution funkcióban általában #NUM értéket kapunk! a szórás argumentum miatti hiba kisebb vagy egyenlő nullával.

Ajánlott cikkek

Ez egy útmutató az Excel NORMSINV-hez. Itt megvitatjuk, hogyan lehet a NORMSINV-t Excelben használni, a gyakorlati példákkal és a letölthető Excel sablonnal együtt. Megnézheti más javasolt cikkeinket -

1. Hogyan lehet használni a név mezőt az Excelben?
2. Munka a Matrix programmal Excelben
3. Mi van, ha az elemzés Excelben?
4. NPV képlet Excelben