
Bevezetés a beszúrásba Rendezés a JavaScript-ben
A rendezés az egyik legfontosabb fogalom, amelyet a programozók megtanulnak a számítógépes tudomány útja megkezdéséhez, függetlenül attól, hogy milyen programozási nyelvet választottak a tanuláshoz. A válogatás segít felkeresni kívánt cégadatok gyorsabb és kényelmesebb megtalálását növekvő vagy csökkenő sorrendben.
A rendezési algoritmusokat az elemek átrendezéséhez használják, ahol az elem lehet szám vagy karakterlánc. A válogatás módszere és az elemek rendezéséhez alkalmazott megközelítés alapján sokféle rendezési algoritmus létezik, és mindegyik típusnak megvannak az előnyei és hátrányai.
Ebben a blogban a beszúrási rendezésre összpontosítunk, ez egy általános, könnyen megérthető és megvalósítható rendezési módszer.
Mi az a beszúrásfajta a JavaScript-ben?
A beszúrási rendezés egy egyszerű, könnyen érthető algoritmus, amely egy kis adateljesítmény esetén a legjobban működik, ha az adatlistában minden elemet balról jobbra rendezi egyenként. Összehasonlítási rendezésként is ismert, ahol összehasonlítja az aktuális értéket a rendezett adatlista többi értékével. Egy iteratív megközelítést követ az egyes elemek megfelelő sorrendbe helyezése az adatlistában.
Minél több időt vesz igénybe egy algoritmus rendezése, a teljesítményét rossznak mondják, és az adatok rendezéséhez másik algoritmust kell fontolóra vennie. A beszúrási sorrend időbeli bonyolultsága O (n²), vagy másodrendű idő fut az adatlista rendezéséhez a legrosszabb eset esetén. Ez általában nem túl hatékony, ezért nem szabad nagy listákhoz használni. Általában azonban felülmúlja a fejlettebb algoritmusokat, mint például a gyorslista vagy az egyesítés a kisebb listákon.
Beillesztési rendezés, az idő nagy részében hatékonyabb, mint más másodlagos rendezési algoritmusok, például buborék rendezés vagy szelekciós rendezés. Legjobb esetben az idő O (n) vagy lineáris, ami akkor fordul elő, ha a bemeneti tömb már rendezve van. Átlagosan a beszúrási sorrend futási ideje még mindig másodlagos.
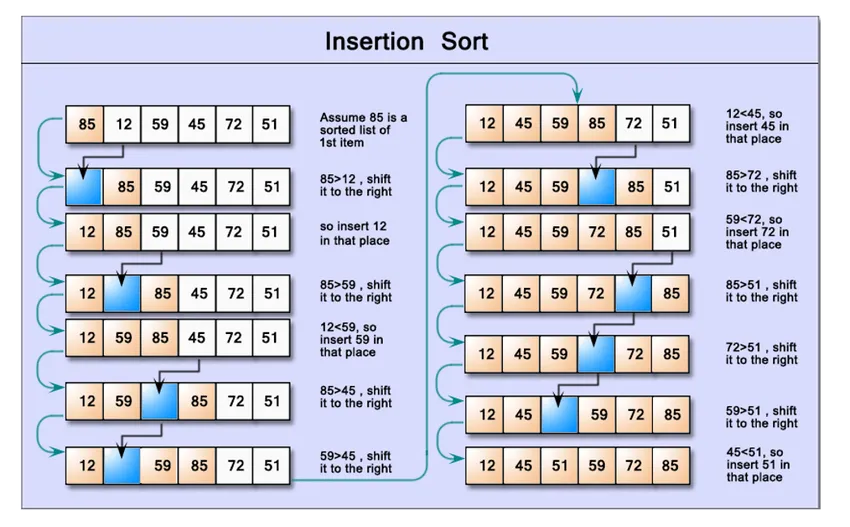
Az alábbi példában egy egyszerű, magas szintű megközelítést alkalmazunk a tömb adatszerkezetében tárolt adatok rendezésére, és a rendezési módszerrel az adatok rendezésére algoritmusok végrehajtása nélkül.
Példa - Beillesztési rendezési algoritmus
Kód:
// Declaring unsorted data and storing it in array data structure
var dataArray = (96, 5, 42, 1, 6, 37, 21) // Function - Insertion Sort Algo.
function insertSort(unsortedData) (
for (let i = 1; i < unsortedData.length; i++) (
let current = unsortedData(i);
let j;
for(j=i-1; j >= 0 && unsortedData(j) > current;j--) (
unsortedData(j + 1) = unsortedData(j) )
unsortedData(j + 1) = current;
)
return unsortedData;
)
// print sorted array
console.log(insertSort(dataArray));
Kimenet:
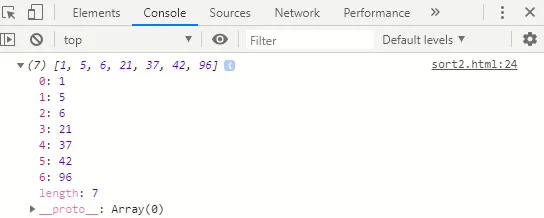
Magyarázat: Az algoritmusban 2-et hajtottunk végre hurkok számára, a hurok számára a külsőnek a tömbelemeken át kell iterálódni, a hurok belső oldalán pedig a tömb elemeit értékük növekvő sorrendjében kell rendezni. Az aktuális változó a tömb aktuális értékét tartja, és a j változót egy értéknél kevesebbre állítja, mint a tömb aktuális indexpozíciója. Ellenőrizzük, hogy az aktuális elem (áram) kisebb-e, mint a j tömbön található tömbérték (unsortedData (j) ), és ha ez igaz, akkor ezeket az értékeket rendezzük.
1. iteráció - áram (96): (96, 5, 42, 1, 6, 37, 21)
2. iteráció - áram (5): (5, 96, 42, 1, 6, 37, 21)
3. iteráció - áram (42): (5, 42, 96, 1, 6, 37, 21)
4. iteráció - áram (1): (1, 5, 42, 96, 6, 37, 21)
5. iteráció - áram (6): (1, 5, 6, 42, 96, 37, 21)
6. iteráció - áram (37): (1, 5, 6, 37, 42, 96, 21)
7. iteráció - áram (21): (1, 5, 6, 21, 37, 42, 96)
A hurok iterációjának külső része az első index pozícióban kezdődik, mivel a legkisebb elemet balra akarjuk mozgatni, tehát összehasonlítjuk, hogy az aktuális elem kisebb-e, mint a bal oldali elem.
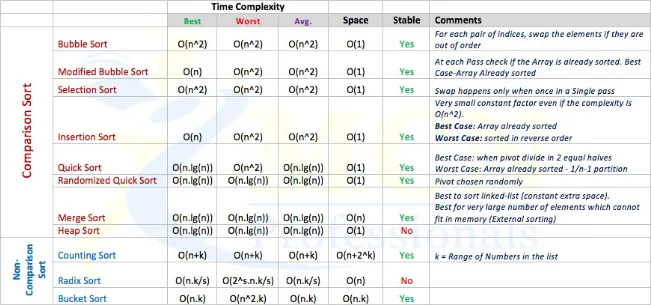
A válogatás típusai
Az algoritmusok típusai, amelyeket az adatok rendezéséhez használnak, az alábbi fogalmakat vagy ötleteket tartalmazzák az adatok rendezésének megközelítésében:
- Összehasonlítás a nem összehasonlításon alapuló stratégiákkal,
- Iteratív versus rekurzív megvalósítás,
- Osztás-és -hódítás paradigma (ez vagy más),
- Véletlenszerű megközelítés.
Nézzük meg néhány példát:
1. A rendezés egyesítése a split-and-conquer megközelítést használja a tömb elemeinek rendezéséhez.
2. Az Insertion Sort, a Bubble Sort egy összehasonlítási alapú rendezés.
Az adatok rendezésekor könnyebb az optimális megoldás megtalálása az összetett problémákra. például,
- Egy adott érték keresése,
- Megtalálja a minimális vagy maximális értéket,
- Az egyediség tesztelése és a másolatok törlése,
- Megszámoljuk egy adott érték hányszor jelent meg stb.
Következtetés
Ebben a cikkben áttekintettük a beszúrási sorrend és az időbonyolultság meghatározását, valamint a megközelítésük alapján számos más rendezési algoritmustípust. Különböző válogatási algoritmusok tanulmányozása segít beazonosítani, hogy melyik megfelelhet bizonyos körülmények között, vagy használhat olyan eseteket, amelyek segítenek az adatok gyorsabb rendezésében.
Ajánlott cikkek
Ez egy útmutató a beszúrási rendezéshez a JavaScript-ben. Itt példával tárgyaljuk, mi a javascript beszúrási típusa és típusai. A következő cikkeket is megnézheti további információkért -
- Minták a JavaScript-ben
- Esetnyilatkozat a JavaScript-ben
- Feltételes kijelentések a JavaScript-ben
- JavaScript objektumok
- Különböző típusú hurkok és azok előnyei