Különbség a lineáris regresszió és a logisztikus regresszió között
A következő cikk: Lineáris regresszió vs. logisztikus regresszió nyújtja a legfontosabb különbségeket mindkettő között, de mielőtt megnézzük, mit jelent a regresszió?
Regresszió
A regresszió alapvetően statisztikai mérőszám az egyik függő változó, azaz az Y kimenet és más független változók sorozata közötti kapcsolat erősségének meghatározására, azaz X 1, X 2 és így tovább. A regressziós elemzést alapvetően a jóslatokra és az előrejelzésekre használják.
Mi az a lineáris regresszió?
A lineáris regresszió egy olyan algoritmus, amely a gépi tanulás felügyelt tanulási tartományán alapul. Lineáris kapcsolatot örököl bemeneti változói és az egyetlen kimeneti változó között, ahol a kimeneti változó folyamatos természetű. A kimenet értékének becslésére szolgál, mondjuk, hogy Y a bemenetek közül, mondjuk X. Ha csak egyetlen bemenetet tekintünk, egyszerű lineáris regressziónak nevezzük.
Két fő kategóriába sorolható:
1. Egyszerű regresszió
Működési elv: A fő cél az egyenes egyenletének kiderítése, amely a legjobban illeszkedik a mintába felvett adatokhoz. Ez az egyenlet algebrai módon leírja a két változó közötti kapcsolatot. A legjobban illeszkedő egyeneset regressziós vonalnak hívják.
Y = β 0 + β 1 X
Hol,
β a tulajdonságokat képviseli
β 0 jelzi az elfogást
β 1 a X tulajdonság együtthatóját jelenti
2. Többváltozós regresszió
Egynél több független változó és egy függő változó közötti korreláció becslésére szolgál. A kettőnél több független változóval történő regresszió az alakot illeti az adatok csillagképéhez egy többdimenziós grafikonon. A regresszió alakjának olyannak kell lennie, hogy minimalizálja a forma távolságát minden adatponttól.
A lineáris kapcsolatmodell matematikai módon ábrázolható az alábbiak szerint:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Hol,
β a tulajdonságokat képviseli
β 0 jelzi az elfogást
β 1 az X 1 jellemző koefficiense
β n az X n tulajdonság koefficiense
A lineáris regresszió előnyei és hátrányai
Az alábbiakban bemutatjuk az előnyöket és hátrányokat:
Előnyök
- Egyszerűségének köszönhetően széles körben használják a jóslatok és következtetések modellezésére.
- Az adatok elemzésére és az adatok előfeldolgozására összpontosít. Tehát különféle adatokkal foglalkozik, anélkül, hogy a modell részleteivel foglalkoznának.
hátrányok
- Hatékonyan működik, ha az adatokat általában szétosztják. Így a hatékony modellezéshez el kell kerülni a kollinearitást.
Mi a logisztikus regresszió?
Ez a regresszió egy formája, amely lehetővé teszi a diszkrét változók előrejelzését folyamatos és diszkrét prediktorok keverékével. Ennek eredményeként a függő változók egyedi átalakulását eredményezi, amely nemcsak a becslési folyamatot, hanem a független változók együtthatóit is befolyásolja. Ugyanazzal a kérdéssel foglalkozik, amelyet a többszörös regresszió tesz, de nincs megoszlási feltételezés a prediktorokról. Logisztikus regresszióban az eredményváltozó bináris. Az elemzés célja több magyarázó változó hatásának felmérése, amelyek lehetnek numerikusak, kategorikusak vagy mindkettő.
A logisztikus regresszió típusai
Az alábbiakban bemutatjuk a logisztikus regresszió 2 típusát:
1. Bináris logisztikus regresszió
Abban az esetben használják, ha a függő változó kétoldalú, azaz olyan, mint egy két ágú fa. Akkor használja, ha a függő változó nem paraméteres.
Használva, amikor
- Ha nincs linearitás
- A függő változónak csak két szintje van.
- Ha a többváltozós normalitás kétséges.
2. Multinomális logisztikus regresszió
A multinomális logisztikus regressziós elemzés megköveteli, hogy a független változók metrikusak vagy kétirányúak legyenek. Nem tesz feltételezést a linearitás, a normalitás és a variancia homogenitása szempontjából a független változók esetében.
Akkor használják, ha a függő változónak kétnél több kategóriája van. A nem metrikus függő változó és a metrikus vagy dikotóm független változók közötti kapcsolatok elemzésére szolgál, majd összehasonlít több csoportot bináris logisztikus regresszió kombinációjával. Végül együttmûködési együtthatókkal szolgál mind a két összehasonlításhoz. A referenciacsoport együtthatóinak minden nullát figyelembe kell venni. Végül az előrejelzést a legmagasabb eredményszintű valószínűség alapján végezzük.
A logisztikus regresszió előnye: Ez egy nagyon hatékony és széles körben alkalmazott technika, mivel nem igényel sok számítási erőforrást és hangolást.
A logisztikus regresszió hátránya: Nem alkalmazható nemlineáris problémák megoldására.
A fej közötti összehasonlítás a lineáris regresszió és a logisztikus regresszió között (Infographics)
Az alábbiakban bemutatjuk a 6 legfontosabb különbséget a Lineáris Regresszió és a Logisztikus Regresszió között 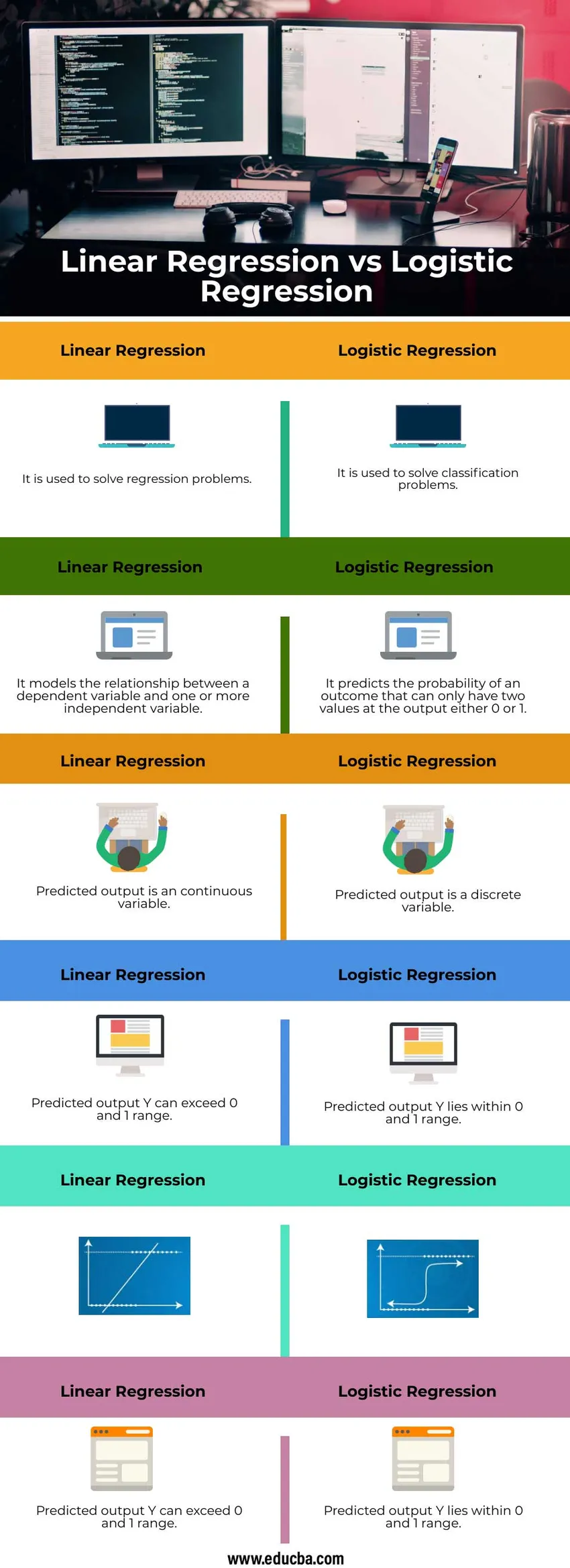
Legfontosabb különbség a lineáris regresszió és a logisztikus regresszió között
Beszéljünk néhány főbb különbségről a Lineáris Regresszió és a Logisztikus Regresszió között
Lineáris regresszió
- Ez egy lineáris megközelítés
- Egyenes vonalat használ
- Nem lehet kategorikus változókat venni
- Figyelembe kell venni a megfigyeléseket, ahol hiányzik a numerikus független változó értékei
- Az Y kimenetet így kell megadni
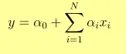
- X egységnyi növekedése növeli Y-t α-val
Alkalmazások
- A termék árának előrejelzése
- A mérkőzés eredményének előrejelzése
Logisztikus regresszió
- Ez statisztikai megközelítés
- Szigmoid függvényt használ
- Ez kategorikus változókat igényelhet
- Még akkor is hozhat döntéseket, ha hiányzó értékekkel rendelkező megfigyelések vannak jelen
- Az Y kimenetet úgy kell megadni, mint ahol z van megadva
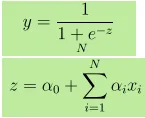
- X egységnyi növekedése növeli Y-t α log-esélyével
- Ha P egy esemény valószínűsége, akkor (1-P) annak valószínűsége, hogy nem történik meg. Sikeres esélyek = P / 1-P
Alkalmazások
- Annak előrejelzése, hogy ma esik-e vagy sem.
- Annak előrejelzése, hogy az e-mail spam vagy sem.
Lineáris regresszió vs logisztikus regresszió összehasonlító táblázat
Beszéljük meg a lineáris regresszió és a logisztikus regresszió legfelső összehasonlítását
|
Lineáris regresszió |
Logisztikus regresszió |
| A regressziós problémák megoldására szolgál | Az osztályozási problémák megoldására szolgál |
| A függő változó és egy vagy több független változó kapcsolatát modellezi | Megjósolja egy olyan eredmény valószínűségét, amelynek csak két értéke lehet a kimeneten: 0 vagy 1 |
| A várható output folyamatos változó | A becsült output diszkrét változó |
| A várható Y kimenet meghaladhatja a 0 és 1 tartományt | A várható Y kimenet 0 és 1 tartományon belülre esik |
 | 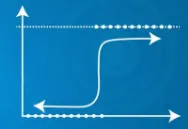 |
| A várható Y kimenet meghaladhatja a 0 és 1 tartományt | Várható output |
Következtetés
Ha a jellemzők nem járulnak hozzá az előrejelzéshez, vagy ha ezek nagyon korrelálnak egymással, akkor ez zajt kölcsönöz a modellnek. Tehát azokat a funkciókat, amelyek nem eléggé járulnak hozzá a modellhez, el kell távolítani. Ha a független változók szorosan korrelálnak, akkor a multi-kollinearitás problémáját okozhatja, amelyet úgy lehet megoldani, hogy az egyes független változókon külön modelleket futtatunk.
Ajánlott cikkek
Ez egy útmutató a Lineáris Regresszió vs Logisztikus Regresszió szakaszhoz. Itt tárgyaljuk a Lineáris Regresszió vs Logisztikus Regresszió kulcsfontosságú különbségeket az infographics és az összehasonlító táblázat segítségével. Lehet, hogy megnézi a következő cikkeket is, ha többet szeretne megtudni -
- Data Science vs Data Visualization
- Gépi tanulás vs neurális hálózat
- Felügyelt tanulás vs mély tanulás
- Logisztikus regresszió R-ben