
Bevezetés a Matlab inline funkciójába
A Matlab inline funkciói két kategóriába sorolhatók: az egyik beépített függvények, a második pedig a felhasználó által létrehozott meghatározott funkciók.
Beépített funkciók
A Matlab-nak számos beépített funkciója van a négyzetgyök, sin, cos, tan, exponenciális, log stb.. Ezenkívül bonyolultabb és speciális matematikai funkciókat is tartalmaz, például gamma- és Bessel-függvényeket. Van néhány beépített konstans a pi, I (komplex számok) és a végtelenséggel.
Példa:
sin ( pi / 2 )
1-es eredményt ad.
ebben a példában a pi értékét nem is említettük, automatikusan a pi értéke 3.14.
sqrt (3)
1, 73 eredményt ad.
És ha az sqrt (-1) program-nyilatkozatot írjuk, akkor az ans értéke 0, 00 + i

Felhasználó által definiált funkciók
A kulcsszó a „inline” függvény meghatározásához szolgál, most nézzük meg, hogyan kell használni
Tegyük fel, hogy szeretnék létrehozni egy fun = x 2 - 6 függvényt
A Matlab parancsok lesznek
Fun = inline ( ' x 2 – 6 ', ' x ' ) . . . . . . . . . . (1) function declaration and defination
Fun =
inline function :
Szórakozás = - 6.. . . . . . kimenete (1)
Fun ( 1 ) (2) giving value x=1
Ans =
-5. . . . (2) kimenete
Fun ( 2 ) ….(3) giving value x=2
Ans =
-2 . . output (3)
Fun ( 3 ) . . . . . . . . . . . . . . . . . . . . (2) giving value x=3
ans =
3. . . . . . output (3)

- A Matlab funkciók skaláron és vektorokon is működnek
- Az inline funkció győzelmeinek eléréséhez a 'vectorize' kulcsszót használjuk a funkció meghatározásán belül.
- Tegyük fel, hogy a fenti példában 'fun' vektorfunkciót akarok létrehozni, akkor a parancsok lesznek
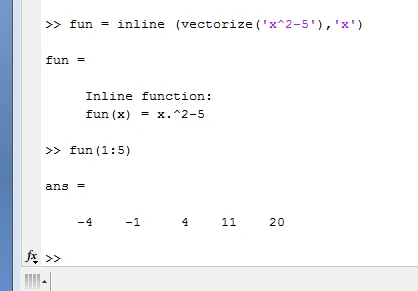
Fun = inline ( vectorize ( ' x 2 – 5 ', ' x ' )
Ez vektor móka.
Fun ( 1 : 5 )
And evolution will take values of x as 1, 2, 3, 4 and 5
Ennek a programnak a kimenete lesz
-4-1 4 11 és 20
Ebben az első érték x = 1, a második érték x = 2, harmadik érték x = 3, a negyedik érték x = 4 és az ötödik érték x = 5.
Az inline függvény szintaxisa
Ez három kategóriába sorolható.
1. Funkció meghatározása: Ebben írjuk a függvény karakterláncot és definiáljuk a független változót.
Function name = inline ( ' function ', ' independent variable ' )
Fun = inline ( ' x 2 – 5 ', ' x ' )
2. Funkció evolúció: Ebben az esetben úgy értékeljük a függvényt, hogy bármilyen értéket megadunk a független változónak.
Function name (variable value )
Fun ( 1 )
3. Vektorizáló függvény: Ez a függvény létrehozza az adott függvény vektorát.
Function name = inline ( vectorize( ' function string ' ), ' independent variable ' )
Y = inline ( vectorize ( ' x 2 – 1 ' ), ' x ' )
Példák
A következő példák a következők
1. példa:
Vegyünk egy funkciót
Z = x 3 - 56
A fenti egyenlet Matlab-ban történő megoldásához létre kell hoznunk egy in-függvényt z-hez, és hozzá kell rendelnünk egy független változót.
Matlab kód:
>>
z =
Inline function :
Z ( x ) = x . 3 - 56
>> z ( 0 )
Ans = 4
>> z ( 1 0 )
Ans = 996
>> z ( -1 )
Ans = 5
2. példa:
Z = x 3 + 23 x - 9
Matlab kód például 2
Z = inline ( vectorize ( ' x .^3 + 23*x – 9 ' ), ' x ' )
z =
Inline function :
Z ( x ) = x . 3 + 23 * x - 9
>> z ( 1 : 10 )
Ans = 1–3. Oszlop
15 45 87
4–6. Oszlop
147 231 345
7–9. Oszlop
495 687 927
10. oszlop
1221
>> z ( 1 : 0.5 : 5 )
Ans = 1–4. Oszlop
15.0000 28.8750 45.0000 64.1250
5–8. Oszlop
87.0000 114.3750 147.0000 185.6250
9. oszlop
231.0000
Következtetés - Inline funkciók a Matlabban
Az inline funkciók globálisak, de soha nem foglal helyet a Matlab munkaterületen. Úgy működik, mint anonim függvények, de ezek nem anonim függvények, mivel az anonim függvények helyet foglalnak el a funkció létrehozásakor. Az inline függvények csak egy értéket adnak vissza tömbökkel és mátrixokkal foglalkozó rendszerben.
Ajánlott cikkek
Ez egy útmutató a Matlab beépített funkcióihoz. Itt a Matlab, a Szintaxis és a Példák inline funkcióit tárgyaljuk. Megnézheti más kapcsolódó cikkeinket, hogy többet megtudjon-
- Mi a Matlab?
- Bevezetés a Matlabba
- Matlab parancsok
- Karrier a MATLAB-ban
- Matlab fordító | A Matlab Compiler alkalmazásai
- Példák a Python beépített funkcióira