Excel Lineáris Interpoláció (Tartalomjegyzék)
- Mi az interpoláció?
- Interpoláció az előrejelzési függvénnyel az Excelben
- Példák az lineáris interpolációra Excelben
Mi az interpoláció?
A matematika világában az interpoláció ismert adatpontok segítségével új adatpontok létrehozásának módszere. Az interpoláció becsli az értéket a rendelkezésre álló, elérhető relációs adatok alapján.
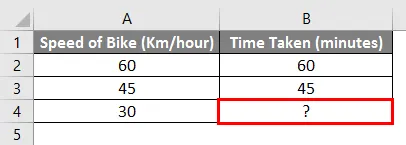
Példa: Ha egy kerékpárral 60 Km / órás sebességgel haladunk meg, és egy órán belül elértünk egy adott célállomást, és ha 45 Km / óra sebességgel haladunk, és egy 45 perc alatt elértünk egy adott célállomást. Tehát mennyi időt vesz igénybe egy rendeltetési hely elérése, ha 30 km / h sebességgel haladunk.
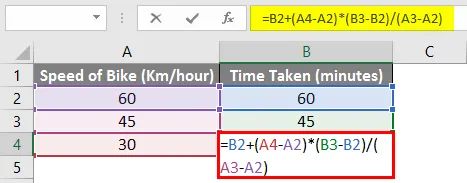
Az egyszerű matematika segítségével kiszámolhatjuk a hiányzó értékeket a fenti példában. Be kell illesztenünk az alábbi képletet a B4 cellába.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Tehát a fenti képlet alapján elmondhatjuk, hogy 30 percig tart, amíg 30 km / órás sebességgel haladunk az úticél felé.
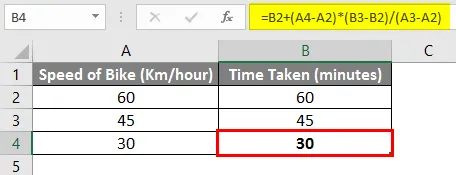
Próbáljuk megbontani a fenti képletet és megértsük a képletet részletesen.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
A fenti példában a képlet utolsó szakaszában, amelyet vörös színű kiemeléssel számolunk, mennyi idő változik, amikor a kerékpár sebessége 1-rel változik. Példánkban az eltelt idő 1 perccel változik, amikor a kerékpár sebessége 1 km-rel változik. /óra.
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
A második szakasz (a fenti kék színnel) kiszámítja, hogy a kerékpár sebessége milyen messze van a megadott első sebességtől, majd megszorozzuk a fent kiszámított értékkel. Példánk szerint ez 30 (A4-es cella) mínusz 60 (A2-cella), ennek eredményét megszorozzuk 1-gyel (ami -30).
= B2 + (A4-A2) * (B3-B2) / (A3-A2)
Végül a képlet első szakasza (fentebb barnával); hozzáadjuk a kerékpár sebességének első értékét. Példánkban ez a végső eredmény 60 + (-30) * (1) = 30 perc. Az iskolában az alábbi képletet használtuk a hiányzó Y érték kiszámításához.
Y = Y1 + (X-X1) * (Y2-Y1) / (X2 - X1)
Ez egy példa arra, hogyan lehet kiszámítani a hiányzó értékeket kézi képlet segítségével az interpoláció megértéséhez.
Az Excelnek van egy beépített függvénye, amely a fentiekhez hasonló számítást végez, és FORGÁLAT funkcióként ismert. Most részletesen megtanuljuk ezt a funkciót.
Interpoláció az előrejelzési függvénnyel Excelben
Az előrejelzés egy munkalap-függvény, amely elérhető az MS Excel programban, és a hiányzó érték kiszámításához lineáris regressziót használ. Az előrejelzés, amint a neve is sugallja, egy adatpont jövőbeni értékének előrejelzésére szolgál, de felhasználható egy érték interpolálására is. Alapvetően arra használják, hogy a jövőbeni értéket kiszámítsák egy adott adatkészlet létező értékei alapján.
Az előrejelzési függvény szintaxisa

Az előrejelzés funkciójának érvei:
- x - Ez egy olyan adatpont, amelyhez meg akarjuk tudni az eredményül kapott értéket.
- Ismert_y-k - Az Y értékeket tartalmazó cellatartomány.
- Ismert_x - az X értékeket tartalmazó cellatartomány.
Most, figyelembe véve a fenti példát, próbáljuk meg használni az Előrejelzés funkciót.
Példánkban
x - B4 cella (mivel meg akarjuk tudni, hogy mennyi időt vesz igénybe, ha a sebesség 30 km / óra).
Ismert_yek - B2-cella - B3-as cella (a kerékpár ismert sebességéhez szükséges idő).
Ismert_x - A2 cellából az A3 cellába (a már megadott kerékpár sebessége, amelyre tudjuk az időt).
Tehát a B4 cellában a következő képlet lesz az alábbiak:
= FORECAST (A4, B2: B3, A2: A3)
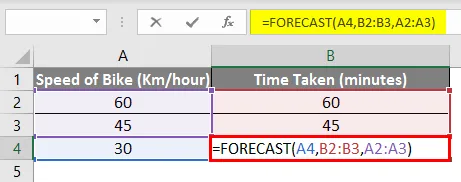
És amint láthatja, a végeredmény ugyanaz, azaz 30 perc .
Diagram készítéséhez lépjen az Insert menübe, kattintson a Scatter elemre, majd válassza a Scatter With Smooth Line and Markers lehetőséget.
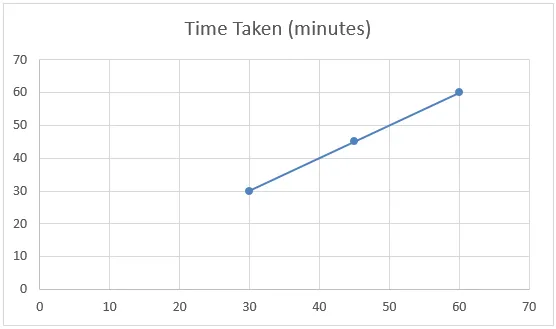
Ha megnézzük a fenti példa alábbi diagramját, akkor azt mondhatjuk, hogy az adatkészletnek lineáris összefüggése van, és lineáris interpolációnak nevezzük.
Példák az lineáris interpolációra Excelben
Nézzük meg néhány példával az Lineáris Interpolációt Excelben.
Itt letöltheti ezt a Lineáris Interpolációs Excel sablont - Lineáris Interpolációs Excel sablon1. példa
Tegyük fel, hogy rendelkezik az előző évek eladási és nyereségadataival, és meg szeretné tudni, hogy egy adott értékesítési szint elérésekor a tárgyév nyeresége van.
Nézze meg az alábbi táblázatot. 2016 és 2018 közötti értékesítési adatai vannak, és szeretné tudni, hogy mi lehet a profit, ha az értékesítés Rs. 40, 00 000 2019-ben.
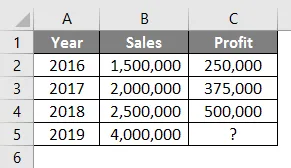
Tehát az Előrejelzés funkció segítségével interpolálhatjuk a 2019-es eredményt, amikor az értékesítés Rs. 4000000
A C5 cellában szereplő képlet az alábbiak szerint alakul:
= ELŐNYÖK (B5, C2: C4, B2: B4)
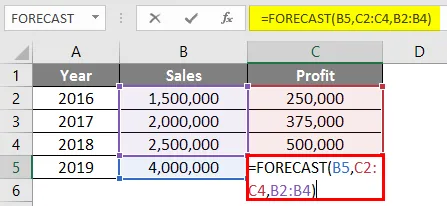
Az előrejelzési képlet használata után az alább látható válasz.
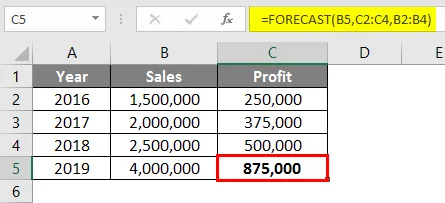
Az Előrejelzés funkció eredménye Rs. 875 000, a 2016 és 2018 közötti időszakra rendelkezésre álló értékesítési és profit adatok alapján.
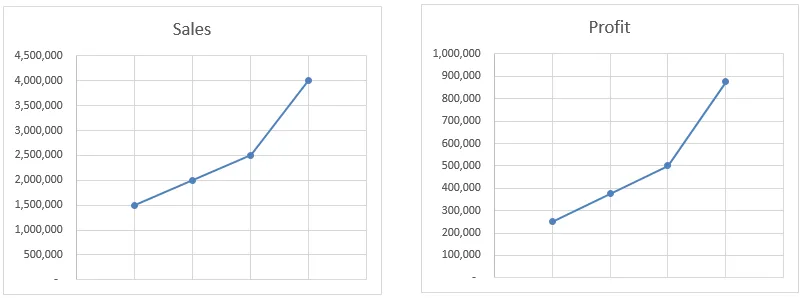
Ebben a példában az Előrejelzés funkció az összes rendelkezésre álló adat alapján interpolálja az értéket, nem csak a kezdőpontot és a végpontot. Mint láthatja a táblázatokban, a profit mozogása pontosan megegyezik az eladásokkal. Még ha manuálisan is kiszámoljuk az értéket, akkor is ugyanazt az eredményt fogja kapni.
2. példa
A krikettcsapat utolsó 9 mérkőzésének adatai rendelkeznek, mivel a kapuk elmentek és a csapat pontozta.
Meg akarjuk tudni, hogy hány futást eredményez a csapat, ha 8 kapu esik.
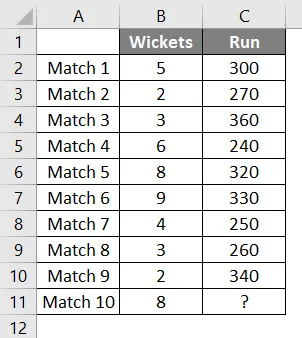
Tehát ismét ugyanazt az előrejelzési függvényt fogjuk használni, mint a fentiekben.
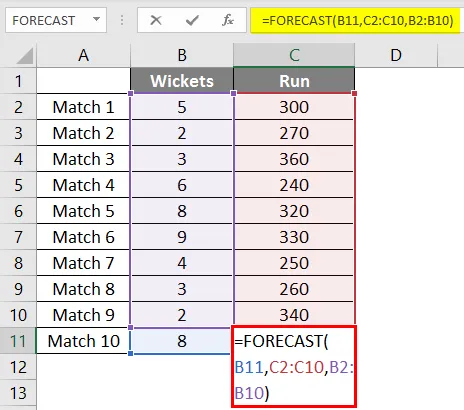
A képlet alkalmazása után megkapjuk a 302 futtatás eredményét, ha 8 kapunk esik a csapat utolsó 9 mérkőzésének lineáris regressziója alapján.
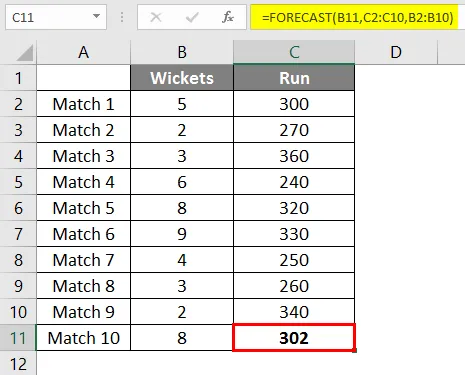
Ebben a példában az adatok nem voltak lineárisak, és ezt az alábbi grafikonon láthatja. De az előrejelzés funkció még a korábbi mérkőzések adataival segített bevonni a futásokat.
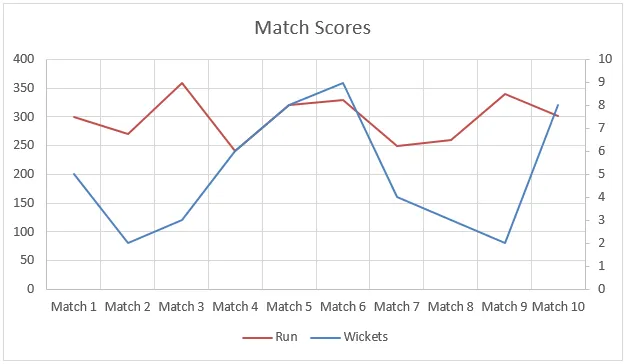
Ne felejtse el az lineáris interpolációt az Excel programban
- Az előrejelzés funkció az érték előrejelzésére / becslésére szolgál a rendelkezésre álló értékek alapján, de segíthet a hiányzó érték interpolálásában is.
- Ha az adatok nem lineárisak, az Előrejelzés funkció nem adja meg a pontos értéket, amely lineáris interpoláción alapszik, de a legközelebbi értéket adja meg.
- Ha az Forecast függvényben x szöveg vagy nem numerikus, akkor az Forecast funkció visszatér a #VALUE hibához.
- Ha a Known_x és a Known_y nem tartalmaz semmilyen adatot, vagy eltérő adatpontot tartalmaz, az Előrejelzési függvény # N / A hibát fog adni.
- Ha az ismert_x szórása nulla, akkor az Előrejelzés függvény # DIV / O hibát ad.
Ajánlott cikkek
Ez egy útmutató az Lineáris Interpolációhoz Excelben. Itt tárgyaljuk, hogyan lehet a Lineáris Interpolációt használni az Excelben, valamint a gyakorlati példákat és a letölthető Excel sablont. Megnézheti más javasolt cikkeinket -
- Lineáris regresszió az Excelben
- Keressen szöveget az Excel programban
- Szöveges képlet Excelben
- Marimekko Chart Excel
- Interpoláció az Excel programban
- Lineáris programozás Excelben