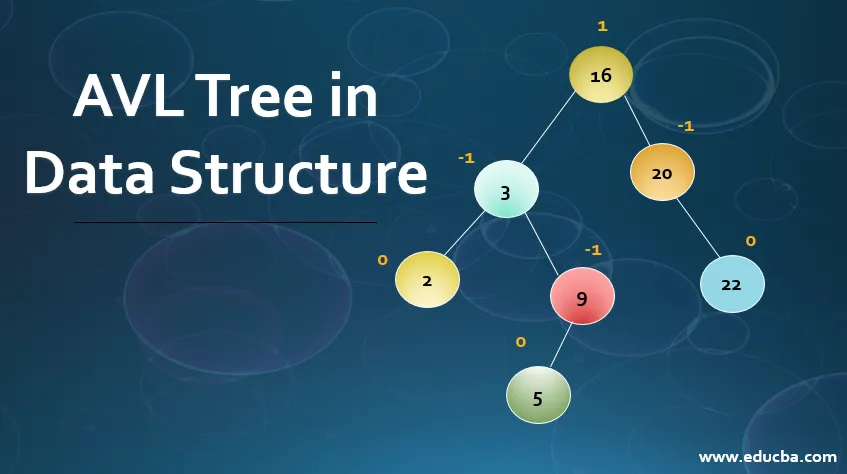
Bevezetés az AVL fa adatszerkezetébe
Az AVL fa az adatszerkezetben Adelson, Velski és Landis fara utal. Ez a bináris keresési fa továbbfejlesztett változata. Az összes tulajdonsága a bináris keresési fahoz hasonló, de csak abban különbözik egymástól, hogy fenntartsák a különbséget a bal alfa és a jobb alfa közötti magasság között, és azt is biztosítják, hogy az értéke <= 1 a fában, ez az egyensúly Tényező.
Balance Factor = height(left-subtree) − height(right-subtree)
Például: Vegye figyelembe a következő fákat

A fenti példában a jobb alfa = 2 és a bal = 3 magassága, tehát BF = 2, azaz <= 1, tehát a fa kiegyensúlyozott.
Miért van szükségünk AVL fára DS-ben?
A bináris keresési fával való együttműködés során szembesülünk egy forgatókönyvvel, ahol az elemek rendezett sorrendben vannak. Ilyen esetekben a tömb összes eleme a gyökér egyik oldalán van elrendezve, ez növeli az elem tömbben történő keresésének időbeli összetettségét, és a bonyolultság O -vé válik (n), vagyis a fa legrosszabb összetettsége. . Az ilyen kérdések megoldása és a keresési idő csökkentése érdekében AVL fákat Adelson, Velski & Landis talált fel.
Példa:

A fenti ábrán a bal alfák magassága = 3 olyan volt, mint a
A jobb részfák magassága = 0
Így egyensúlyi tényező = 3-0 = 3. Így egy elem keresése egy ilyen fában O (n) bonyolultságával rendelkezik, ami hasonló a lineáris kereséshez. A komplex keresés elkerülése érdekében bevezették az AVL-fát, ahol a fa minden csomópontját meg kell tartani
egyensúlyi tényező <= 1, különben különféle forgási technikákat kell végrehajtani az ilyen fa kiegyensúlyozására.
Struct AVLNode
(
int data;
struct AVLNode *left, *right;
int ball factor;
);
Forgás típusai
Ha a fa egyensúlyi tényezője nem felel meg <= 1 feltételnek, akkor forgatásokat kell végrehajtani rájuk, hogy kiegyensúlyozott fává váljon.
4 típusú forgás létezik:
1. Bal forgás: Ha egy csomópont hozzáadása a fa jobb oldalán egyensúlyhiányt okoz, akkor ebben az esetben a Bal forgatást kell végrehajtani.
2. Jobb forgás: Ha egy csomópont hozzáadása a fa bal oldalához egyensúlyhiányt okoz, akkor a jobb forgatást végre kell hajtani. Más szavakkal: Ha a csomópontok száma a bal oldalon növekszik, akkor szükség van az elemek jobb oldalra tolására, hogy kiegyenlítsék, tehát azt mondják, hogy jobb forgás.
3. Bal és jobb forgás: Az ilyen típusú forgatás a fenti 2 magyarázat szerinti kombináció. Ez a fajta forgás akkor fordul elő, amikor egy elemet hozzáadunk a bal fa jobb alsó részéhez.
Ebben az esetben először hajtsa végre a bal oldali forgást a részfán, majd kövesse a bal fa jobb forgását.
4. Jobbra-balra forgás: Az ilyen típusú forgás egy 2-nél nagyobb forgási sorozatból is áll. Ez a fajta forgás akkor szükséges, ha egy elemet adunk a jobb oldali alfához balra, és a fa kiegyensúlyozatlanná válik. Ilyen esetben először a jobb oldali részszéren végezzük el a jobb forgást, majd a jobb oldalon a bal oldali forgást.
Műveletek AVL fán DS-ben
Az AVL fán végrehajtható 3 művelet alatt: -
1. Keresés
Ez a művelet hasonló a keresés végrehajtásához a bináris keresési fában. Az alábbiak szerint járnak el:
- Olvassa el azt az elemet, amelyet a felhasználó mond x.
- Hasonlítsa össze az elemet a gyökérből, ha ugyanaz, akkor lépjen ki, ellenkező esetben lépjen a következő lépésre.
- Ha x
Másik a jobb gyermekhez jár, és hasonlítsa össze újra.
Kövesse a B és a C folyamatot, amíg meg nem találja az elemet és kilép.
Ennek a folyamatnak O (log n) bonyolultsága van.
Példa:
 | Fontolja meg ezt a fát, ahol meg kell keresnünk a 9. csomópont értéket. Először hagyjuk x = 9, gyökérérték (12)> x, akkor az értéknek a gyökér elem bal részében kell lennie. |
 | Most x-et hasonlítjuk össze a 3. csomópont értékével x> 3, tehát a jobb részbél felé kell haladnunk. |
 | Most x-et hasonlítottuk össze a (9) csomóponttal, ahol 9 == 9 visszatér igaz. Így az elemkeresés befejeződik a fában. |
2. Helyezze be
Miközben egy elemet beilleszt az AVL fába, meg kell találnunk a beilleszteni kívánt helyhez tartozó elemet, majd az elemet ugyanúgy csatolni kell, mint a BST-be, de utána megvizsgáljuk, hogy a fa továbbra is kiegyensúlyozott-e vagy sem. azaz egy csomópont egyensúlyi tényezője <= 1. És bizonyos forgásokat szükség szerint hajtunk végre.
A komplexitás O (log n).
Példa: Vegyük figyelembe az alábbi fát,
 | Minden csomópont egyensúlyi tényezője 0, -1 vagy 1, tehát a fa kiegyensúlyozott. Most lehetővé teszi, hogy mi történjen, ha egy 1. értékű csomópont kerül beillesztésre. Az első fát áthaladva megtalálja azt a helyet, ahol be kell helyezni… Az 1 <2 tehát a csomópont bal gyermekeként van írva (2). |
 | A beillesztés után a (9) csomópont kiegyenlítetlenné válik, ha egyensúlyi tényezője = 2. Most jobb forgatásnak vetik alá. |
 | A fa egyensúlyba kerül a jobb forgás után, és így a beszúrási művelet sikeresen befejeződik. |
3. Törlés
Az elem törlése az AVL fából magában foglalja egy elem keresését a fában, majd törlését. A keresési művelet megegyezik a BST-vel, és a törlendő elem megtalálása után az elemet eltávolítják a fáról, és az elemeket úgy állítják be, hogy ismét BST legyen. Miután ezeket az elemeket ellenőriztük, hogy 0, -1 vagy 1 egyensúlyi tényezőjük van-e, és így megfelelő forgatásokat hajtunk végre, hogy kiegyensúlyozott legyen.
Komplexitás, ha O (log n).
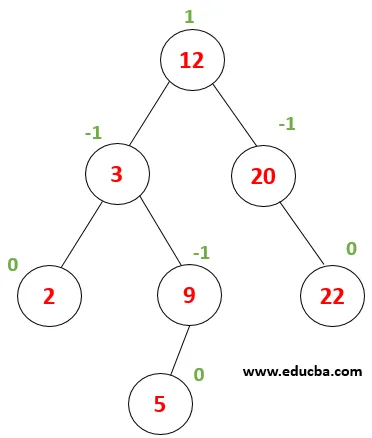
 | Vegyük figyelembe az adott fát, amelynek egyensúlyi tényezője 0, -1 vagy 1. Töröljünk egy 16-as csomópontot. Az első fán átkerül a 16. értékű csomópont megkeresése, amely megegyezik a keresési algoritmussal. |
 | A 16. csomópont helyébe ennek a csomópontnak a bemeneti elődje lép, amely a legnagyobb elem a bal alfából, azaz 12 A fa kiegyensúlyozatlanná vált, ezért LL-forgást kell végrehajtani. |
 | Most minden csomópont kiegyensúlyozott. |
Következtetés - AVL fa az adatszerkezetben
Az AVL fa a bináris keresési fa leszármazottja, de legyőzi annak hátrányát, hogy növekvő összetettséggel jár, ha az elemeket rendezik. Figyelemmel kíséri a fa egyensúlyi tényezőjét 0 vagy 1 vagy -1-re. Abban az esetben, ha a fa kiegyensúlyozatlanná válik, a megfelelő egyensúlyozáshoz forgási technikákat hajtanak végre.
Ajánlott cikkek
Ez egy útmutató az AVL fa adatstruktúrájához. Itt tárgyaljuk a Bevezetést, az AVL-fán végzett műveleteket a DS-ben és a forgatások típusait. Megnézheti más kapcsolódó cikkeket is, ahol többet megtudhat -
- jQuery Elements
- Mi az adattudomány?
- A fák típusai az adatszerkezetben
- C # Adattípusok