
Bevezetés a Python Fibonacci sorozatába
A Pythonban található Fibonacci sorozatot ez számsornak nevezi, ahol a következő szám a jelenlegi két szám összege.
Például:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 .. így tovább
Tehát itt 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 és így tovább.
A fentiek alapján némi elképzelésünk lenne arról, miről beszélünk.
A matematikai szabályt azonban így lehet megfogalmazni:

Az n-edik szám a (n-1) és (n-2) helyek számának összege. A Fibonacci sorozat megvalósításakor számos kódoló nyelv létezhet, amelyen keresztül meg lehet valósítani.
A Python azonban manapság széles körben használt nyelv. Lássuk a Fibonacci sorozat megvalósítását Pythonon keresztül. Az itt folytatás előtt tisztában kell lennie az alapvető kondicionáló kijelentésekkel, mint például a hurok, ha más, míg a hurok stb. Pythonban. Ha nem, nagyszerű lenne, ha felülvizsgálja, majd átveszi a következő tartalmat. Demó céljára spyder-et használok, amely IDE a python programozási nyelvhez. Bármely más IDE vagy Ipython notebook felhasználható a Python programok végrehajtására.
Fibonacci sorozat Pythonban
Lássuk a Fibonacci szám és sorozat megvalósítását, figyelembe véve a Fibonacci első két elemét: 0 és 1:
A Fibonacci funkcióját azonban módosíthatja a követelményei szerint, de először megnézheti az alapokat, és fokozatosan tovább léphet mások felé.
Python-kód az n. Fibonacci-szám megtalálására
1. kód:
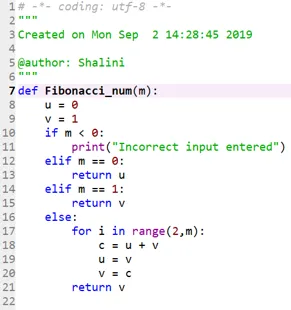
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
2. kód:
Kimenet:
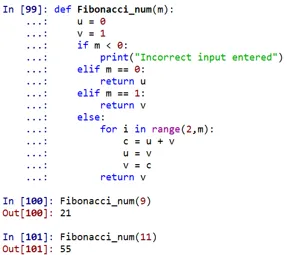
Mint látható, a 9. helyen a Fibonacci-szám 21, a 11. helyen 55 lenne.
- Itt a „fibonacci_num” egy definiált függvény, amely bizonyos körülmények között gondoskodik a Fibonacci szám megtalálásáról. Ezt a funkciót bármilyen helyzet megadásával meg lehet hívni.
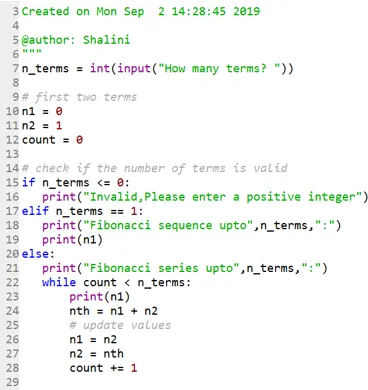
Most nézzük meg, hogyan lehet sorozatot kinyomtatni az említett pozícióig:
Kód:
Kimenet:
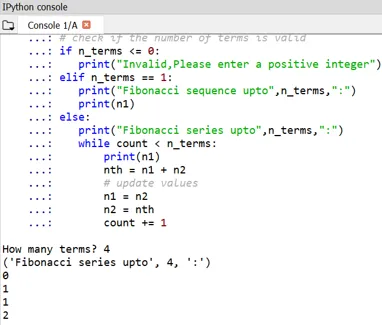
Megfigyelhető a Fibonacci-számok kezdetének 0 és 1 értéke.
- Ha valaki meg akarja határozni a saját kiindulási feltételeit, akkor ezt ugyanúgy meg lehet tenni az n1 és n2 hozzáigazításával. Íme a példa erre:
Tegyük fel most, hogy azt akarjuk, hogy a kiindulási feltételek: n1 = 3, n2 = 5
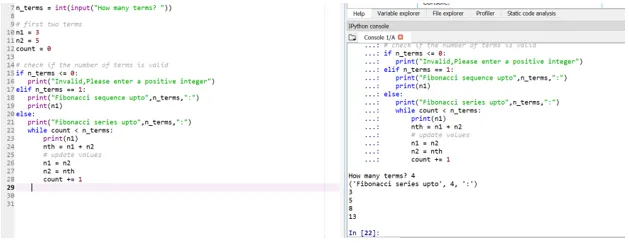
Tehát itt a 4. ciklus pozícióját (a felhasználói bevitel megtörtént) a kiindulási feltételek alapján döntenek.
Módszerek, amelyek révén a Fibonacci sorozat előállítható
Az alábbiakban bemutatjuk a három módszert, amellyel a Fibonacci sorozat generálható:
1. Generátorokon keresztül
Kód:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Kimenet:
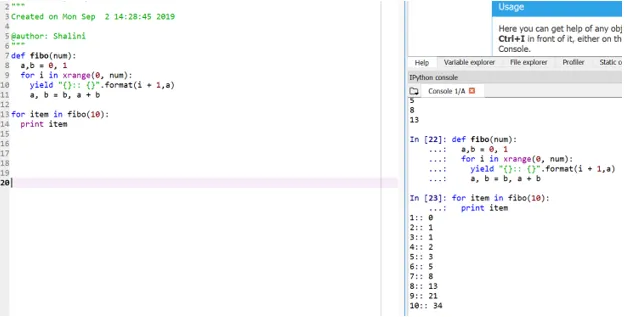
Ezt a módszert „generátornak” nevezzük, mivel az xrange függvény 0 és num közötti szám generátor, a hozam pedig a formázott kimenet generátora.
Itt van, mit jelent az xrange az Ön számára:

Itt a Fibonacci sorozatot a függvény formájában határoztuk meg, amelyben a hurok, az xrange és a hozam függvény gondoskodik a kimenetről.
2. Hurokig
Kód:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Kimenet:

Mint látható, a hurok egyszerűvé vált a 0 és 10 közötti Fibonacci sorozat kinyomtatásához. A hurok belsejében új értékeket rendeltek a változókhoz. U és v a Fibonacci alapértelmezett kezdeti értékei, amelyek 0-ra, illetve 1-re vannak beállítva.
Ami a hurok futását halad, az új u érték a régi v érték, míg az új v érték a régi u és v értékének összege. Ez a tartományértékek végéig folytatódik.
3. rekurzión keresztül
Kód:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Kimenet:
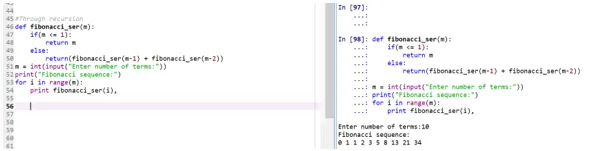
- A „fibonacci_ser” funkció felhívja magát a Fibonacci sorozat kinyomtatására.
- És ezért a módszer elnevezése „rekurzió”.
Itt követett lépések:
- Itt a felhasználót arra kérték, hogy adja meg azt a helyet, ameddig a Fibonacci sorozatot ki kell nyomtatni.
- A szám áthalad a „fibonacci_ser” függvényen.
- Ellenőrizzük az állapotot, ha a megadott hosszúság kevesebb, mint 1. Ha igen, az eredményt azonnal megkapják.
- Ha azonban a hossza nagyobb, mint 1, akkor rekurzív hívásokat kezdeményezünk a „fibonacci_ser” -re olyan érvekkel, amelyek hossza kisebb, mint 1 és 2, azaz fibonacci_ser (m-1) és fibonacci_ser (m-2).
- Ezért a rekurzió megadja a kívánt eredményt és kinyomtatja.
- Tehát röviden, a Fibonacci sorozat megjelenítésének három módjáról beszélgettünk.
- Hurokon keresztül, generátorokon keresztül és rekurzión keresztül.
Mindhárom Python-kód összefoglalva
Az alábbiakban található a három python kód:
1. Generátorokon keresztül
Kód:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Hurokig
Kód:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. rekurzión keresztül
Kód:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
A fentiekben összegeztük az összes eljárást, gyakorlást kell végezni ahhoz, hogy mindenki jól megfogjon.
Kimenet:
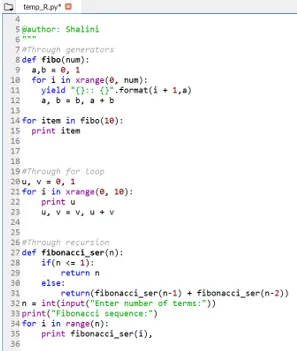
Következtetés
A fenti Fibonacci-tartalom áttekintésével kristálytiszta megértést kaphatott volna a pythonra szakosodott Fibonacci-számok és sorozatok. Egyszer kényelmesebbé válik a Fibonacci sorozat logikája, újabb sorozatkészítést generál, más számokkal és különféle módszerekkel dolgozik, ez most az Ön számára vándorlás lesz. A logikus megközelítés az egyetlen módja annak, hogy kitűnjön ebben.
Ajánlott cikkek
Ez egy útmutató a Python Fibonacci sorozatához. Itt a Fibonacci számokat és sorozatokat tárgyaljuk, amelyek a pythonra szakosodtak, újabb sorozatot generálnak, más számokkal és különféle módszerekkel dolgoznak. Megnézheti más kapcsolódó cikkeket is, ha többet szeretne megtudni -
- Véletlenszám-generátor Pythonban
- Matematikai funkciók a Pythonban
- Faktérium a Pythonban
- Beágyazás a Pythonba
- Fibonacci sorozat Java-ban
- Python szolgáltatások
- Faktorialis program a JavaScript-ben
- Véletlenszám-generátor a Matlab-ban
- Véletlenszám-generátor C # -ben
- Beágyazás a JavaScript-be