
Bevezetés a matematikai funkciókba C
Ez a cikk felsorolja a C programozási nyelvekben használt különféle matematikai függvényeket a működési kód szemléltetésével. A számítógépek hatalmas matematikai számításokat végeznek és hatalmas számok elemzését végezték el. Ehhez a C matematikai tulajdonságait használtuk. Mielőtt elkezdenénk, meg kell ismernünk a C nyelveket, amelyek a Math.h nevű fejléc / könyvtárat használják a különféle matematikai függvényekhez. Ez segít kiszámítani a trigonometrikus műveleteket, logaritmusokat, abszolút értékeket, négyzetgyökereket. Tehát vizsgáljuk meg a könyvtárban használt különféle típusú funkciókat. Mindezek a funkciók adattípusként kettős formátumúak, és ugyanazok visszaadódnak.
Különféle matematikai funkciók a C-ben
Lássuk a math.h-ban meghatározott különböző függvényeket, és a Math könyvtárat három fő típusba soroljuk: trigonometrikus függvények, matematikai függvények, naplózás / expo függvények. Az alábbi funkciók megvalósításához kötelező a kód beírása.
1. emelet (dupla a)
Ez a függvény a legnagyobb egész értéket adja vissza, amely nem haladja meg az 'a' értéket. Kerekít egy értéket, és kettős értéket eredményez. Másképp viselkedik a negatív számoknál, mivel a következő negatív számra kereknek.
Pl .: a padló (7.2) 7, 0
padló (-7, 2) -8, 0
Példa:
Ez a program bemutatja, hogyan lehet kiszámítani a padlót a deklarált értékre és a következő 10 értékre kerekíteni.
#include
#include
int main()
(
double f= -9.33;
int final;
final = floor(f);
printf("Floor value of %.2f = %d", f, final);
return 0;
)
Kimenet:

2. ceil ()
Szintaxis:
double ceil (double b)
Ez a funkció a legkisebb egész értéket adja vissza, amely nagyobb vagy egyenlő b-vel, és felfelé kerekíti. Negatív érték esetén balra mozog. A 3.4 példa szerint a -3 visszatérés rendelkezik a kimenettel.
Példa:
Ez a program azzal magyarázható, hogy beírja a float argumentumot, és visszaadja a ceil értéket.
#include
#include
int main()
(
float n, ceilVal;
printf(" Enter any Numeric element : ");
scanf("%f", &n);
ceilVal = ceil(n);
printf("\n The Value of %.2f = %.4f ", n, ceilVal);
return 0;
)
Kimenet:

3. Sqrt ()
Ez a függvény egy megadott szám négyzetgyökét adja vissza.
Szintaxis:
sqrt( arg)
Példa:
Az alábbi kód a sqrt () matematikai függvényt ismerteti úgy, hogy 'n' értékeket vesz ki a négyzetgyök kiszámításához a különféle 'n' értékekre.
#include
#include
int main()
(
double n, output;
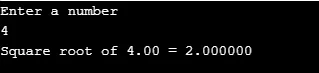
printf("Enter a number\n");
scanf("%lf", &n);
output = sqrt(n);
printf("Square root of %.2lf = %f", n, output);
return 0;
Kimenet:
4. kerek ()
Ez a funkció egy adott bemenet legközelebbi értékét kerekíti. Kihúzza a hibát, ha az érték túl nagy. Más funkciók, például a föld (), az llround () szintén a legközelebbi egészet kerekítik.
Szintaxis:
int round(arg)
Példa:
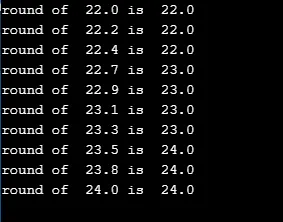
Az alábbi kód nagyon egyszerű, amely a legközelebbi „r” értékre kerekíti a for hurokban.
#include
#include
int main ()
(
for(double r=110;r<=120;r+=1.1)
printf("round of %.1lf is %.1lf\n", r/5.0, round(r/5.0));
return 0;)
Kimenet:
5.pow ()
Ez a funkció visszatér az adott számra (a b ). Visszaadja az emelt értéket b értékének, amelynek két paramétere van az alapjával és az exponenssel.
Példa:
Az alábbi forráskódban megengedjük a felhasználónak, hogy megadjon egy bemeneti értéket az adott két argumentum teljesítményének kiszámításához.
#include
#include
int main()
(
int r, ba, expr;
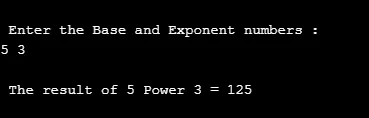
printf("\n Enter the Base and Exponent numbers : \n");
scanf("%d %d", &ba, &expr);
r = pow(ba, expr);
printf("\n The result of %d Power %d = %d ", ba, expr, r);
return 0;
)
Kimenet:
6. csomagtartó ()
Ez a funkció segíti az adott érték csonkítását. Egész számértéket ad vissza. A lebegő és kettős értékek csonkításához a truncf (), a truncl () értékeket használjuk.
Szintaxis:
double trunc(a);
Példa:
A forráskód alatt két a, b bemeneti érték vesz igénybe a kettős értékek csonkítását.
#include
#include
void main() (
double m, n, a, b;
a = 56.16;
b = 85.74;
m = trunc(a);
n = trunc(b);
printf("The value of a: %lf\n", m);
printf("The value of a: %lf\n", n);
)
Kimenet:

7. fmod ()
Ez a függvény adja meg a megadott két bemeneti érték fennmaradó részét, ha m osztva n-kel.
Szintaxis:
double fmod(double I, double j)
Példa:
Az alábbi példában két értékre van szükség a felhasználótól, hogy kiszámolja a maradékot az fmod () függvény segítségével.
#include
#include
int main()(
double fiN;
double secN;
double n;
printf("Enter the first number : ");
scanf("%lf", &fiN);
printf("Enter the second number : ");
scanf("%lf", &secN);
printf("fmod(firstNumber, secondNumber) is %lf \n", fmod(fiN, secN));
)
Kimenet:

Trigonometrikus függvények
Az alábbiakban bemutatjuk a trigonometria különféle funkcióit:
1. bűn ()
Ez a beépített funkció megadja az adott szám szinuszértékét, kiszámítja a lebegőpontos értékeket. Az asin () kiszámítja az ív értéket, a hiperbolikus esetében pedig a sinh ().
Szintaxis:
return type sin(y);
y az értéket sugárban adja vissza, és a visszatérés típusa kétszeresét veszi fel.
Példa:
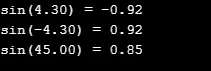
A következő forráskódban két különböző bemeneti értéket vettem a sin érték kiszámításához, és kettős eredményt ad.
#include
#include
int main()
(
double a;
double z;
a = 4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = -4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = 45;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
return 0;
)
Kimenet:
2. sinh ()
Ez a matematikai függvény kiszámítja az adott szám trigonometrikus érintő szinuszértékét.
Szintaxis:
double sinh(x);
Példa
Az alábbi forráskódban a szinusz hiperbolikát egy bemeneti érték deklarálásával számolják.
#include
#include
#define PI 3.141592654
int main()
(
double gt = 3.60, z;
z = sinh(gt);
printf("Sine hyperbolic of %.2lf is = %.2lf", gt, z);
return 0;
)
Kimenet

3. cos ()
Ez a matematikai függvény határozza meg az adott elem trigonometrikus koszinus értékét.
Szintaxis: return type cos(argument);
#include
#include
#define PI 3.14
int main()
(
double cVal, rVal, dVal;
for(int i=0;i<=2;i++)
(
printf(" Enter an Angle in degrees : ");
scanf("%lf", &dVal);
rVal = dVal * (PI/180);
cVal = cos(rVal);
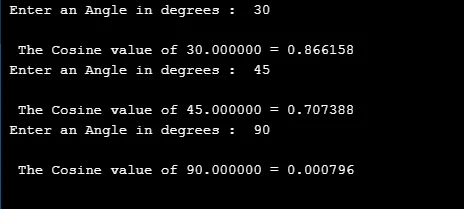
printf("\n The Cosine value of %f = %f ", dVal, cVal);
printf("\n");
)
return 0;
)
Kimenet:
4. cosh ()
Egy adott értékre hiberbolikus koszinust ad vissza.
Szintaxis:
double cosh(y);
Példa
Az alábbi példa azt mutatja, hogy két különböző bemeneti értékre van szükség a hiperbolikus kiszámításához.
#include
#include
int main ()
(
double k, r;
k = 0.6;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
k = -0.8;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
return 0;)
Kimenet

5. tan ()
Ez a matematikai könyvtár függvény kiszámítja a matematikai kifejezés szögének érintőjét és a sugárban mért értéket.
Megadható
double tan(arguments);
Példa
A következő forráskódban a tan értékét kiszámítják a következő szögekhez, amelyeket a hurok használatával növelnek.
# include
# include
# include
void main()
(
float z ;
int k ;
char ch ;
printf("\nAngle \t Tan \n") ;
for (k = 0; k <= 180; k = k + 30)
(
z = k * 3.14159 / 180 ;
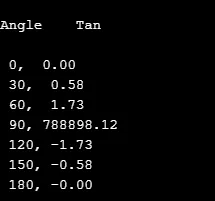
printf("\n %d, %5.2f", k, tan(z));
)
getch() ;
)
Kimenet:
6. tanh ()
A tanh () függvény az adott érték hiperbolikus érintőjét adja vissza. Ez egyetlen paramétert igényel. A hosszú kettős érintőjének megtalálása mellett a számításhoz a tanhlt () és a tanhfot () kell használni.
Szintaxis:
double tanh( val);
Példa:
A „j” értékek érintő hiberbolikusát számítják ki a hurkok felhasználásával. Lássuk, hogyan működik.
#include
#include
#define PI 3.141592654
int main()
(
double val, r;
for(double j=0.60; j<=2.0;j+=.30)
(
r = tanh(j);
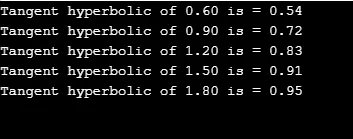
printf("Tangent hyperbolic of %.2lf is = %.2lf", j, r);
printf("\n");
)
return 0;
)
Kimenet:
Naplózási számtani függvények
Az alábbiakban bemutatjuk a naplózási számtani különböző funkciókat:
1. exp ()
Ez a függvény kiszámítja az exponenciális értéket egy adott értékre (e x ). Vannak más altípusok is, mint például a frexp (), az Idexp (), amely visszatér a mantissát és megszorozzuk x erejéig.
Szintaxis:
return type exp(value);
Példa:
A program számértéket vesz a felhasználótól az exponens kiszámításához egy adott értékre, és duplán tér vissza.
#include
#include
int main()
(
double numb, eVal;
printf(" Enter any Numeric Value : ");
scanf("%lf", &numb);
eVal = exp(numb);
printf("\n Exponential Value of e power %lf = %lf ", numb, eVal);
printf("\n");
return 0;
)
Kimenet

2. napló ()
Ez a függvény egy adott szám logaritmusértékét adja vissza. (az alaphoz. napló e )
Szintaxis:
double log(arg);
Példa:
A következő példában az adott szám log értékét a függvény segítségével számoljuk ki. Az lgm () felhasználó által definiált függvény elvégzi a számítást, és a függvényt meghívjuk a fő függvényben.
#include
#include
float lgm ( float iv );
int main ()
(
float q, r ;
printf ( "\nEnter a number to find log value \n");
scanf ( "%f", &q ) ;
r = lgm ( q ) ;
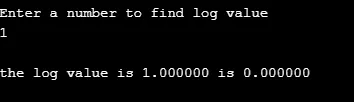
printf ( "\nthe log value is %f is %f", q, r );
)
float lgm ( float iv ) // function definition
(
float exe ;
exe = log(iv);
return ( exe ) ;
)
Kimenet:
Következtetés
Összegezve: láthattunk különféle matematikai függvényeket, amelyeket a C programozásban használnak, és ezek a közvetlen könyvtári függvények. A C programok ezeket a funkciókat különféle matematikai műveletekhez használják. A számítások komplex változatainak megoldására ez a beépített funkció elősegíti a matematikailag orientált programozási nyelvet, hogy visszatérjen az egyszerű értékekhez.
Ajánlott cikkek
Ez egy útmutató a C matematikai függvényekhez. Itt példákkal tárgyaljuk a C matematikai funkcióit. Megnézheti más javasolt cikkeinket -
- PHP matematikai funkciók
- JavaScript matematikai funkciók
- Funkciók átvitele a Matlab-ban
- JavaScript karakterlánc-funkciók
- Bevezetés a matematikai funkciókba a Pythonban
- A C # matematikai funkcióinak áttekintése
- C Programozó mátrix szorzás
- Négyzetgyökér a PHP-ben
- Példák a négyzetgyökérre a JavaScript-ben