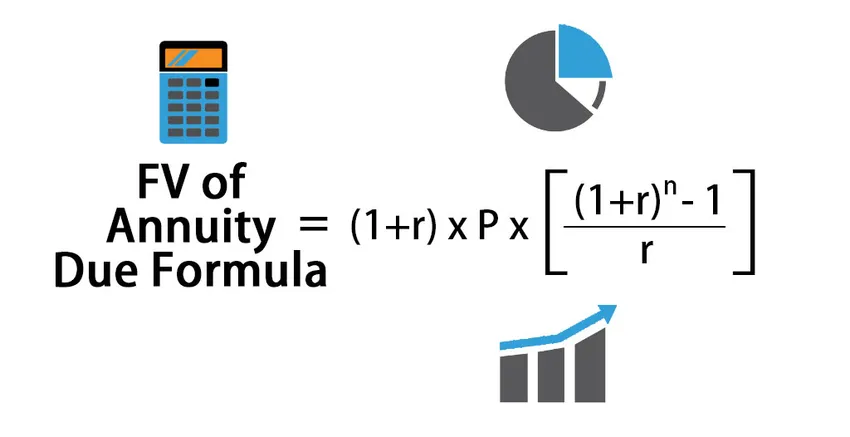
A járadék esedékességi képletének jövőbeli értéke (Tartalomjegyzék)
- A járadék esedékességi képletének jövőbeli értéke
- Példák a járadékra eső képlet jövőbeli értékére (Excel sablonnal)
- A járadék esedékes képletszámológépének jövőbeli értéke
A járadék esedékességi képletének jövőbeli értéke
A fizetendő járadék jövőbeni értékének kiszámítására szolgáló képlet:
FV of Annuity Due = (1+r) * P * (((1+r) n – 1) / r )
Hol,
- P = időszakos fizetés
- R = időszakonkénti ráta
- N = periódusok száma
Példák a járadékra eső képlet jövőbeli értékére (Excel sablonnal)
Vegyünk egy példát, hogy jobban megértsük a járadék jövőbeni értékének kiszámítását.
Itt töltheti le a járadék esedékességi képlete Excel sablonját - A járadék esedékességi képlete Excel sablon1. példa
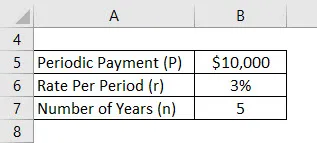
Tegyük fel, hogy egy Anand évente 10 000 dollárt fizetett be, és számlája által kínált tényleges kamatláb 3%. Most Anand 5 év után szeretné kiszámítani jövőbeni egyenlegét az első betét felvételével a mai naptól kezdve.
Megoldás:
A fizetendő járadék jövőbeni értékét az alábbiakban megadott képlettel kell kiszámítani
Esedékes járadék FV = (1 + r) * P * (((1 + r) n - 1) / r)
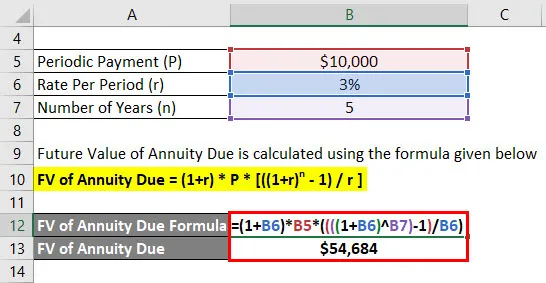
- Esedékes járadék FV = (1+ 3%) * 10 000 USD * (((((1 + 3%) 5) - 1) / 3%)
- Esedékes járadék FV = 54 684 USD
Anand 5 68 év után 54 684 dolláros jövőbeli egyenleget fog keresni.
2. példa
Tegyük fel, hogy egy Jagriti évente 8000 dollárt fizetett be, és számlája által kínált tényleges kamatláb 5%. Jagriti most 5 éven belül ki akarja számítani jövőbeni egyenlegét az első betét felvételével, a mai naptól kezdve.

Megoldás:
A fizetendő járadék jövőbeni értékét az alábbiakban megadott képlettel kell kiszámítani
Esedékes járadék FV = (1 + r) * P * (((1 + r) n - 1) / r)
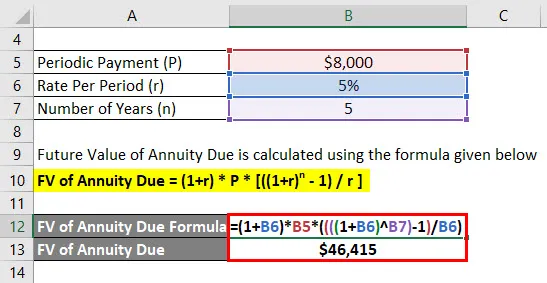
- Esedékes járadék FV = (1+ 5%) * 8000 USD * (((((1 + 5%) 5) - 1) / 5%)
- Esedékes járadék FV = 46 415 USD
Jagriti 46 415 dolláros jövőbeli egyenleget fog szerezni 5 év után.
3. példa
Tegyük fel, hogy egy Anandriti évente 20 000 dollárt fizetett be, és számlája által kínált tényleges kamatláb 2%. Most Anandriti szeretné kiszámítani jövőbeni egyenlegét öt év után az első betét felvételével, a mai naptól kezdve.
Megoldás:
A fizetendő járadék jövőbeni értékét az alábbiakban megadott képlettel kell kiszámítani
Esedékes járadék FV = (1 + r) * P * (((1 + r) n - 1) / r)
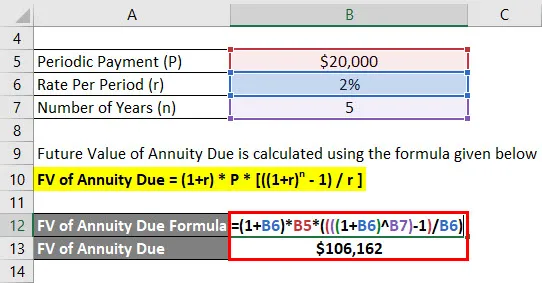
- Esedékes járadék FV = (1+ 2%) * 20 000 USD * (((((1 + 2%) 5) - 1) / 2%)
- Esedékes járadék FV = 1 066 162 USD
Az Anandriti 5 év múlva 1 066 162 dollár egyenleget fog szerezni.
Magyarázat
A pénzáramok vagy fizetések sorozatának záróértékének kiszámításához, ahol az első részlet azonnal megérkezik, a fizetendő járadék jövőbeni értékét használjuk. Az első azonnali részlet vagy kifizetés megkülönbözteti a rendes járadék miatt a járadékot. Az azonnali vagy azonnali járadékot esedékes járadéknak nevezik.
Kiszámítja a pénzáramok értékét egy jövőbeli időszakban. A fizetendő járadék FV felhasználása a valós helyzetekben eltér a fizetendő járadék jelenértékétől. Tegyük fel például, hogy egy vállalat vagy egyén járadékot vásárol, és ma kifizette az első részletet. Használhatjuk a példát további magyarázatokhoz, feltételezzük, hogy egy társaság vagy magánszemély bárkinek meg akar vásárolni járadékot, és ma már kifizette az első kifizetést. A fizetendő ár kiszámításához ebben a helyzetben használhatjuk a járadék jelenértékének képletét. Ha azonban számolni akarjuk a fennmaradó egyenleget, miután a számlán öt évre kamatot megtakarítottunk, és úgy döntöttünk, hogy ma kifizeti az első részletet, ebben az esetben a járadék jövőbeli értékét vesszük figyelembe. A fizetendő járadék olyan járadék egyfajtaként magyarázható, ahol a cash flow-k az egyes időszakok elején jelentkeznek. A cash flow-k speciális jellege miatt minden cash flow-t minden további időszakra összetett hatásnak kell kitenni, abban az esetben, ha azt összehasonlítják egy rendes járadékkal. A rendes járadék jövőbeni értéke alacsonyabb, mint a járadék jövőbeni értéke, mivel a járadék jövőbeni értéke egy plusz tényezővel periodikus kamatot kap.
A járadék jövőbeli értékének relevanciája és felhasználása
Megértjük a jövőbeni érték és járadék jelentését külön. A jövőbeli érték azzal magyarázható, hogy a készpénzösszeg összértéke a jövőben fizetendő egy adott napon. A fizetendő járadék a kifizetések sorozatával magyarázható, amelyet az egyes időszakok elején teljesítenek szabályos sorrendben. Ezért a járadék jövőbeni értéke magyarázható a jövőbeni meghatározott időpontban a teljes értékként egy szisztematikus / időszakos fizetési sorozat esetében, ahol a kifizetéseket az egyes időszakok elején teljesítik. Az ilyen típusú tranzakciók és az ilyen fizetési folyamatok láthatók a nyugdíjprogram kedvezményezett számláján. A teljes érték az az összeg, amelyre a jövőbeni kifizetések sorozata növekszik, mivel egy bizonyos kamatmennyiséget feltételeznek, és a jövedelmek fokozatosan növekednek egy adott időszakban. A rendes járadék jövőbeni értékének kiszámítása ezzel megegyezik, de az egyetlen különbség az, hogy hozzáadunk egy további fizetési időszakot, amely a kezdetben készül.
A járadék esedékes képletszámológépének jövőbeli értéke
Használhatja a járadék esedékességének kalkulátorát
| P | |
| r | |
| n | |
| A járadék esedékességi képletének jövőbeli értéke | |
| A járadék esedékességi képletének jövőbeli értéke = | (1 + r) * P * (((1 + r) n - 1) / r) |
| = | (1 +0) * 0 * (((1 +0) 0 -1) / 0) = 0 |
Ajánlott cikkek
Ez egy útmutató a járadék esedékes képletének jövőbeni értékéhez. Itt tárgyaljuk, hogyan lehet kiszámítani a járadék jövőbeni értékét, a gyakorlati példákkal együtt. Biztosítunk egy letölthető excel sablonnal a járadékdíjak jövőbeli értékét is. A következő cikkeket is megnézheti további információkért -
- Útmutató a pénz időértékének képletéhez
- Példák a jelenérték-tényező képletére
- Számológép információs arány képlet
- A működési tőke mértékének képlete