
A variációs együttható képlete (Tartalomjegyzék)
- Képlet
- Példák
Mi a variációs együttható képlet?
A statisztikákban a variációs együtthatót, amelyet CV-nek is neveznek, egy olyan eszköz, amely segít meghatározni, hogy az adatkészlet adatpontjai hogyan oszlanak meg az átlag között. Alapvetően az összes adatpontot először ábrázoljuk, majd a variációs együtthatót használjuk ezen pontok egymástól való szétszóródásának és az átlagnak a mérésére. Tehát elősegíti az adatok megértését és a formájuk megismerését. Ezt az adatkészlet szórásának és az átlagértéknek a hányadosaként számítják ki. A magasabb variációs együttható azt jelenti, hogy nagyobb az adatok szétszóródása a középérték körül. Hasonlóképpen, minél alacsonyabb a variációs együttható értéke, annál kisebb a diszperzió és annál pontosabbak lesznek az eredmények. Még ha a két adatsor átlaga is jelentősen eltér, a variációs együttható nagyon hasznos az adatsorok közötti variáció mértékének összehasonlításához.
A variációs együttható képlete:
Coefficient of Variation = Standard Deviation / Mean
A variációs együttható kiszámításának lépései:
1. lépés: Számítsa ki az adatkészlet átlagát. A középérték az összes érték átlaga, és kiszámítható az összes érték összegének összegzésével, majd az osztással több adatponttal.
2. lépés: Ezután számolja ki az adatkészlet szórását. Ez egy kis időigényes folyamat. A szórás kiszámítható: √ (Σ (X i - X m ) 2 / (n - 1)) . X i az i. Adatpont és X m az adatkészlet átlaga. Alternatív megoldásként az STDEV.S () függvény használatával megtalálhatjuk az excel szórását is.
3. lépés: Ossza el a szórást középértékkel, hogy megkapja a variációs együtthatót.
Példák a variációs együttható képletére (Excel sablonnal)
Vegyünk egy példát a variációs együttható kiszámításának jobb megértésére.
Itt töltheti le a variációs együtthatót tartalmazó képlet Excel sablont - Változási együttható képlet Excel sablonA variációs együttható képlete - 1. példa
Tegyük fel, hogy két A és B adatkészletünk van, és mindegyik 20 véletlenszerű adatpontot tartalmaz. Számítsa ki a variációs együtthatót az X és Y adatkészletre.
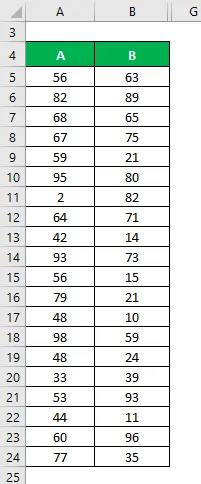
Megoldás:
Az átlag kiszámítása:
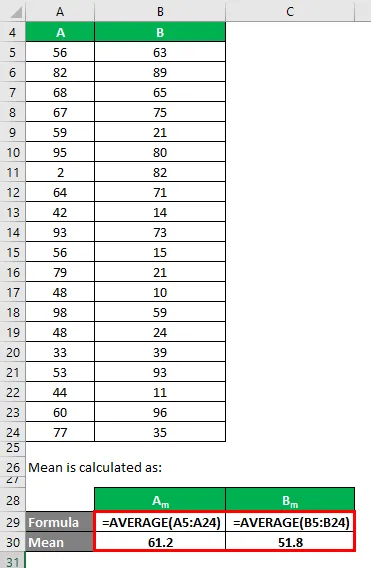
- Az A adatkészlet átlaga = 61, 2
- A B adatkészlet átlaga = 51, 8
Most ki kell számolnunk az adatpontok és az átlagérték közötti különbséget.
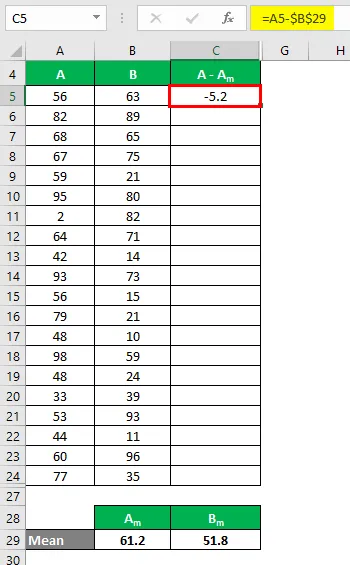
Hasonlóképpen számítsa ki az A adatkészlet összes értékét.
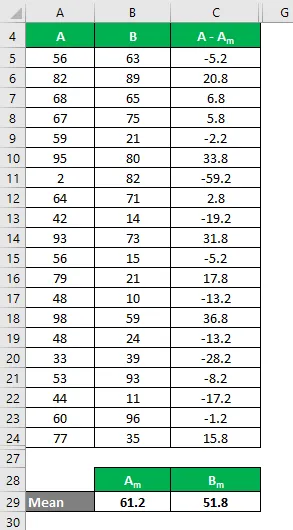
Hasonlóképpen számolja ki a B adatkészlet összes értékét.
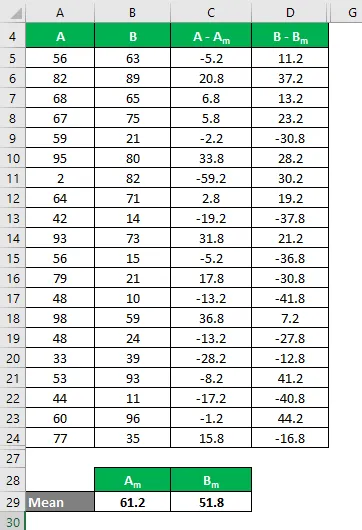
Számítsa ki a különbség négyzetét mind az A, mind a B adatkészletre.
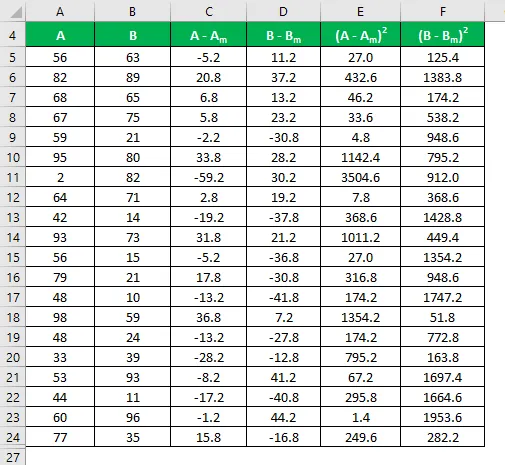
A szórást az alábbiakban megadott képlettel kell kiszámítani
Szabványbeli eltérés = √ (Σ (X i - X m ) 2 / (n - 1))
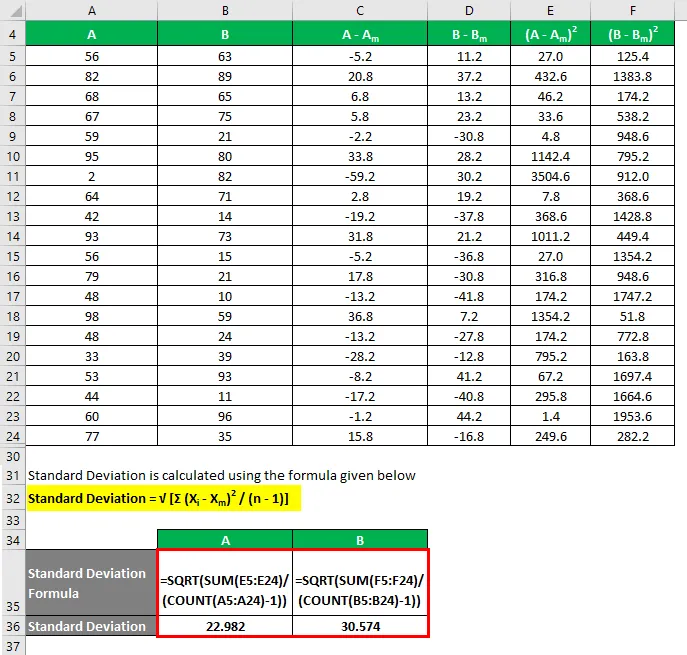
A variációs együtthatót az alábbiakban megadott képlettel kell kiszámítani
Variációs együttható = Szabványos eltérés / Átlag
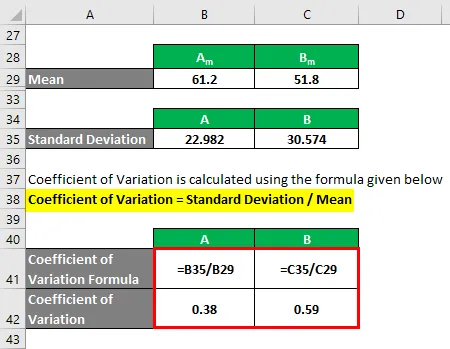
- A variációs együttható = 22, 982 / 61, 2 = 0, 38
- B variációs együttható = 30, 574 / 51, 8 = 0, 59
Tehát ha itt látod, B magasabb variációs együtthatóval rendelkezik, mint A, ami azt jelenti, hogy B adatpontjai szétszórtabbak, mint A.
A variációs együttható képlete - 2. példa
Tegyük fel, hogy nagyon kockázatkerülő befektető, és pénzt szeretne befektetni a tőzsdére. Mivel a kockázatvállalási hajlandósága alacsony, biztonságos részvényekbe szeretne befektetni, amelyek alacsonyabb szórással és variációs együtthatóval rendelkeznek. 3 részvényt választottál az alapvető és technikai információk alapján, és szeretne 2 részvényt választani. Információkat gyűjtött az utóbbi 15 év történelmi visszatéréséről is.
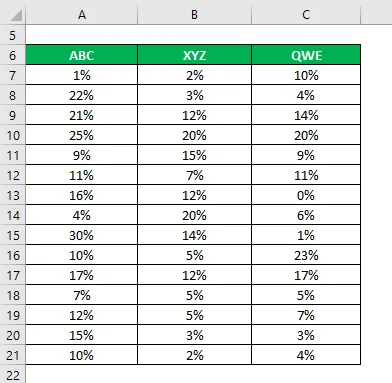
Megoldás:
Az átlag kiszámítása:
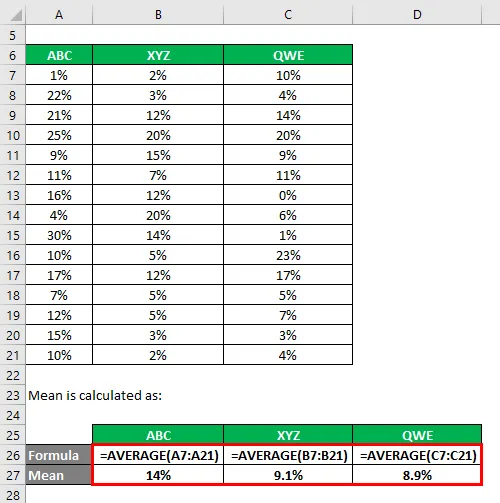
A szórást az excel képlettel kell kiszámítani
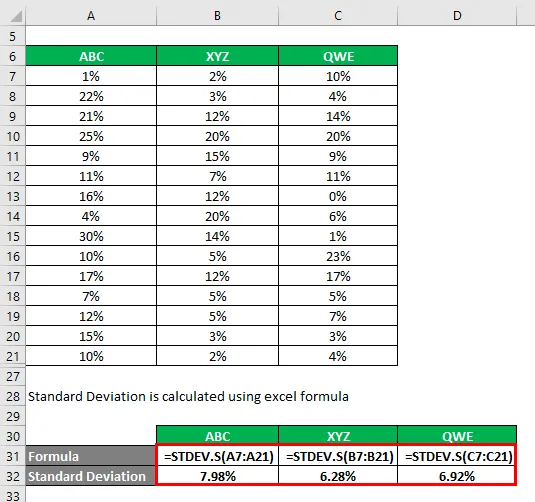
A variációs együtthatót az alábbiakban megadott képlettel kell kiszámítani
Variációs együttható = Szabványos eltérés / Átlag
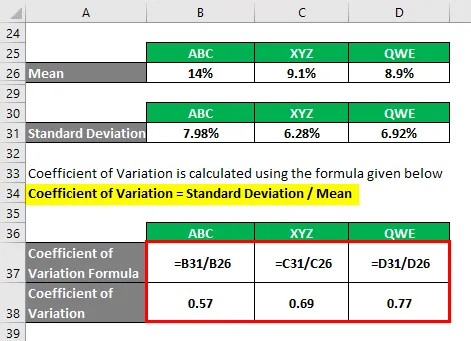
- Az ABC variációs együtthatója = 7, 98% / 14% = 0, 57
- Változási együttható XYZ = 6, 28% / 9, 1% = 0, 69
- Változási együttható QWE = 6, 92% / 8, 9% = 0, 77
Az információk alapján az ABC és az XYZ részvényeket választja befektetni, mivel ezeknek a legalacsonyabb variációs együtthatója van.
Magyarázat
Mivel a variációs együttható a kockázat mérőszáma, elősegíti a részvények és egyéb pénzügyi eszközök árainak ingadozásának mérését. Ezenkívül segíti a befektetőket és az elemzőket a különböző potenciális befektetésekkel kapcsolatos kockázatok összehasonlításában.
A variációs együttható hasonló a szóráshoz, de a két változó szórása nem hasonlítható össze hasznos módon. A szórás és az átlag használata azonban a relatív összehasonlítást értelmesebbé teszi. A variációs együttható korlátozott is. Tegyük fel, hogy egy adatkészlet átlaga nulla. Ebben az esetben ez az eszköz hatástalan lesz. Nemcsak ez, ha van olyan adatkészlet, amelynek számos pozitív és negatív értéke van, a variációs együttható nagyon problematikus. Tehát csak akkor hasznosabb, ha az adatkészletek azonos plusz-mínusz jelet tartalmaznak.
A variációs együttható képletének relevanciája és felhasználása
A variációs együttható a statisztikák kivételével sok más területen releváns. Például a pénzügy területén a variációs együttható a kockázat mérőszáma. Ez hasonló a szóráshoz, mivel ezt a kockázat mérésére is használják, de a különbség az, hogy a variációs együttható jobb mutatója a relatív kockázatnak. Tegyük fel például, hogy A várható hozama 15%, B várható hozama 10%, és A szórása 10%, míg B normál eltérése 5%. Egy jobb befektetés kiválasztásához a variációs együtthatót lehet használni. Tehát A variációs együtthatója 10/15 = 0, 666, és B variációs együtthatója 5/10 = 0, 5. Tehát B jobb befektetés, mint A.
Ajánlott cikkek
Ez egy útmutató a variációs együttható képletéhez. Itt tárgyaljuk, hogyan lehet kiszámítani a variációs együtthatót a képlet segítségével, a gyakorlati példákkal és a letölthető excel sablonnal együtt. A következő cikkeket is megnézheti további információkért -
- Mi az igazított R négyzet formula?
- Példák a meghatározási együttható képletére
- Hogyan számolhatjuk meg a korrelációs együtthatót a képlet segítségével?
- Kovariancia képlet az Excel sablonnal