
Átlagos megtérülési ráta (tartalomjegyzék)
- Átlagos megtérülési ráta
- Példák az átlagos megtérülési ráta képletére (Excel sablonnal)
- Átlagos megtérülési ráta számológép
Átlagos megtérülési ráta
Amint a neve is sugallja, az átlagos megtérülési ráta az átlagos hozam, amelyet várható egy életében beruházásból. Alapvetően az a pénzáramlás összege, amelyet a beruházási időszak során generálnak. Az átlagos megtérülési ráta, más néven a számviteli megtérülési ráta, a beruházási projektek jövedelmezőségének értékelésére szolgáló módszer, amelyet nagyon gyakran használnak a beruházások értékeléséhez. De nem szabad megfeledkeznünk arról, hogy ez a módszer nem veszi figyelembe a pénz időértékét, amely nagyon kritikus tényező a tőkeprojekt értékelésekor. Az átlagos megtérülési rátát úgy lehet kiszámítani, hogy a befektetésből / eszközből várható átlagos hozamot elosztjuk a beruházáshoz szükséges kezdeti pénzzel
Az átlagos megtérülési ráta képlete
Average Rate of Return = Average Annual Profit / Initial Investment
Ahol az éves éves nyereséget kiszámítják:
Éves átlagnyereség = az összes év nyereségének összege / az évek száma
Az átlagos megtérülési ráta kiszámítása
- Az első lépés a beruházás éves profitjának kiderítése. Ezt úgy lehet kiszámítani, hogy kivonjuk az összes szükséges költséget az eladásokból, amelyeket a beruházás során generáltunk
- Meg kell vizsgálnunk, hogy van-e rögzített beruházás, például ingatlan, üzem stb. A projektben. Ha igen, be kell vonnunk az értékcsökkenési költségeket is, és le kell vonnunk azokat az eladásokból
- Ismételje meg ezt az évet, ameddig a projekt tart. Ha már megvan az összes éves profitszáma, keresse meg az átlagos nyereséget az évek számával elosztva. Ezt követően használja ezt az átlagos nyereséget, és ossza meg a beruházás kezdeti költségével
Példák az átlagos megtérülési ráta képletére (Excel sablonnal)
Vegyünk egy példát az átlag megtérülési arány kiszámításának jobb megértésére.
Itt letöltheti ezt a Formula Excel sablon átlagmegtérülési sablonjátÁtlagos megtérülési ráta - 1. példa
Vegyünk egy X kiskereskedelmi céget, amely 1 millió dollárt fektetett be egy olyan projektbe, amelynek élettartama 4 év. A projekt során az alábbiakban látható az éves bölcs profit, amelyet az X keresett:

Az átlagos éves nyereséget az alábbiakban megadott képlettel számolják
Éves átlagnyereség = az összes év nyereségének összege / az évek száma

- Éves átlagos nyereség = (76 000 USD + 45 000 USD + 89 000 USD + 67 000 USD) / 4
- Éves átlagnyereség = 69 250 USD
Az átlagos megtérülési rátát az alábbiakban megadott képlet alapján számítják ki
Átlagos megtérülési ráta = átlagos éves nyereség / kezdeti befektetés
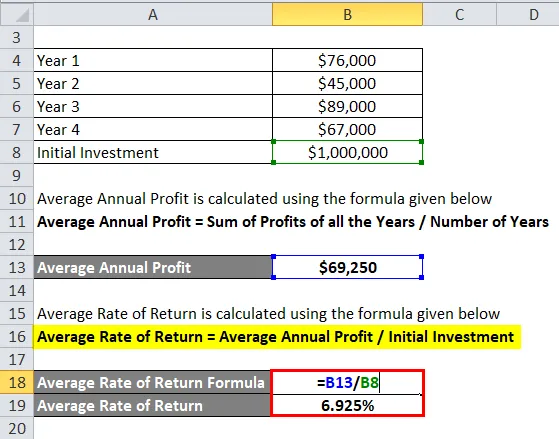
- Átlagos megtérülési ráta = 69 250 USD / 1 000 000 USD
- Átlagos megtérülési ráta = 6.925%
Nem szabad megfeledkeznünk arról, hogy a pénz időértékét itt nem kell figyelembe venni. Tehát az éves cash flow, ha van időértéke, nem fog ugyanazt az értéket megkapni, és jelenértéküknek alacsonyabbnak kell lennie. Tehát például a 45000 USD, amelyet a 2. évben kaptunk, kevesebb lett volna, ha figyelembe vesszük az időértéket.
Átlagos megtérülési ráta - 2. példa
Most lássunk egy másik példát, amely részletesebb. Az XYZ társaság a következő paraméterekkel rendelkező projektet hajtott végre:

Tehát itt az éves nyereséget nem közvetlenül adják meg, hanem a bevétel és a költség felhasználásával lehet kiszámítani.
Az éves várható nyereséget az alábbiakban megadott képlettel számolják
Éves várt nyereség = Bevétel - Költségek
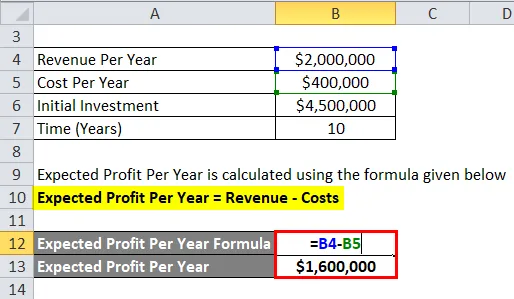
- Éves várt nyereség = 2 000 000 - 400 000 USD
- Éves várható nyereség = 1 600 000 USD
Mivel az egyes évek nyeresége azonos, az átlagos éves nyereség = az éves várt nyereség
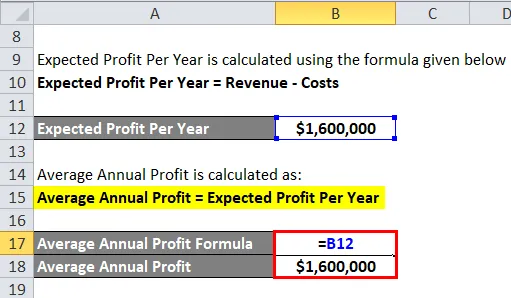
Éves átlagnyereség = 1 600 000 USD
Az átlagos megtérülési rátát az alábbiakban megadott képlet alapján számítják ki
Átlagos megtérülési ráta = átlagos éves nyereség / kezdeti befektetés
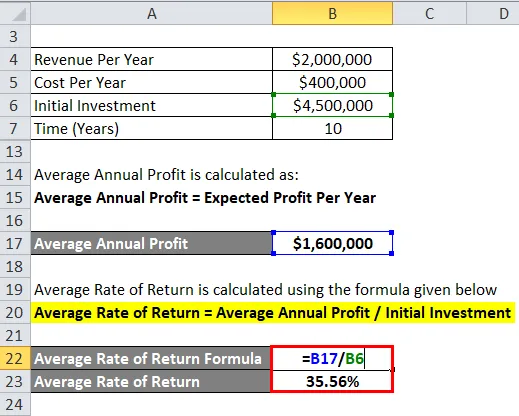
- Átlagos megtérülési ráta = 1 600 000 USD / 4 500 000 USD
- Átlagos megtérülési ráta = 35, 56%
Az átlagos hozamráta képletének magyarázata
Az átlagos megtérülési ráta magas szintű képet ad nekünk a projekt jövedelmezőségéről, és segíthet nekünk abban, hogy érdemes-e beruházni a projektbe, vagy sem. Az átlagos megtérülési ráta beruházási döntések meghozatalához azonban néhány korlátozása van. Lássuk néhány kritikus tényezőt, amelyeket szem előtt kell tartanunk az átlagmegtérülési képlet használatakor
- Mint fentebb megvitattuk, a pénz időértékét az átlagos megtérülési rátában nem vették figyelembe. Ez káros lehet, és arra vezethet, hogy téves befektetési döntést hozzunk. Például: Ha a projekt megtérülési rátája 10% sat, és az átlagos megtérülési ráta 15% lesz, akkor a projekt befektetést érdemel. De miután képet vett a pénzértékekről, a projekt megtérülésének 8% -át mondják. Akkor ez a projekt nem érdemes befektetni
- Másodszor, az átlagos megtérülési ráta nem a tényleges cash flow-n alapul, hanem csak a számviteli információkat használja.
- A másik dolog az, hogy ha két projekt hasonló megtérüléssel rendelkezik, akkor nem különböztethetjük meg ezeket a projekteket a szükséges beruházás nagysága alapján
- Különböző elemzők vagy személyek eltérő módon tudják kiszámítani ezt, tehát a konzisztencia problémája is van
Az átlagos megtérülési ráta képletének relevanciája és felhasználása
Az átlagos megtérülési ráta meglehetősen könnyen érthető és kiszámítható, ha gyorsan meg szeretné tekinteni a projekt jövedelmezőségét. Noha nem veszi figyelembe a pénz időértékét, ez magas szintű képet adhat a projektről. Az alábbiakban néhány előnye van az átlagos megtérülési ráta használatának
- Mint fentebb említettük, nagyon egyszerű kiszámítani és könnyen érthető
- Másodszor, az alapjául szolgáló számviteli információ bárki számára könnyen hozzáférhető és viszonylag könnyen értelmezhető
Dióhéjban, ha egy vállalkozás egy projekttel szeretne kezdeni, és magas szintű képet szeretne látni a projekt jövedelmezőségéről, akkor az átlagos megtérülési rátát lehet használni. És ha ezt a képletet használja, ha a projekt nem érdemes befektetni, akkor selejtezze le a projektet, de ha a projekt jövedelmezőnek tűnik, akkor más paramétereket is meg kell vizsgálniuk, és nem csak az átlagos megtérülési ráta alapján kell támaszkodniuk.
Átlagos megtérülési ráta számológép
Használhatja a következő átlagmegtérülési számológépet.
| Átlagos éves nyereség | |
| Kezdeti beruházás | |
| Átlagos megtérülési ráta | |
| Átlagos megtérülési ráta | = |
|
|
Ajánlott cikkek
Ez egy útmutató az Átlagos megtérülési ráta képletéhez. Itt tárgyaljuk, hogyan lehet kiszámítani az átlagos megtérülési rátát, valamint a gyakorlati példákat. Kínálunk egy letölthető excel sablont az átlagos megtérülési ráta kalkulátorhoz is. A következő cikkeket is megnézheti további információkért -
- Képlet a mérleghez
- Hogyan lehet kiszámítani a hozzájárulási különbözetet?
- A pénzügyi tőkeáttétel képletének kiszámítása
- Számológép a működési fedezeti képlethez
- Hozzájárulás a jövedelemkimutatáshoz