Bevezetés a hierarchikus klaszterezési algoritmusba
A hierarchikus klaszterezési algoritmus nem felügyelt gépi tanulási technika. Célja az adatok jellemzői alapján történő természetes csoportosítás megtalálása.
A hierarchikus klaszterezési algoritmus célja az adatok egymásba ágyazott csoportjainak megtalálása a hierarchia felépítésével. Hasonló a növény- vagy állatvilág biológiai taxonómiájához. A hierarchikus klasztereket általában a dendrogram néven ismert hierarchikus fa segítségével ábrázoljuk.
A hierarchikus klaszterezési algoritmus típusai
A hierarchikus csoportosítási algoritmusok kétféleek:
- Megosztó
- agglomeratív
1. Megosztó
Ez egy felülről lefelé mutató megközelítés, ahol kezdetben a teljes adatokat egy csoportnak tekinti, majd az adatokat iteratív módon felosztja alcsoportokba. Ha a hierarchikus klaszterezési algoritmus száma ismert, akkor a megosztás folyamata leáll, amint a klaszterek száma megtörtént. Máskülönben a folyamat leáll, ha az adatokat nem lehet többé felosztani, ami azt jelenti, hogy az aktuális iterációval kapott alcsoport megegyezik az előző iterációval kapott alcsoporttal (azt is figyelembe lehet venni, hogy az osztódás akkor áll le, ha minden adatpont klaszter ).
2. Agglomerációs
Ez egy alulról felfelé építkező megközelítés, amely a klaszterek összeolvadására támaszkodik. Az adatokat kezdetben m szingulett klaszterekre osztják (ahol m értéke a minták / adatpontok száma). Két klaszter iteratív módon egybeolvadt, ezáltal csökkentve a klaszterek számát minden iterációban. A klaszterek egyesítésének ez a folyamata leáll, ha az összes klaszter összevonásra került, vagy elérte a kívánt klaszterek számát.
Az 1. szinten m klaszterek vannak, amelyek m szintre 1 klaszterre redukálódnak. Azok az adatpontok, amelyek egyesülnek és alacsonyabb szintű klaszterré alakulnak, ugyanazon klaszterben maradnak, a magasabb szinteken is. Tegyük fel például, hogy 8 pont x1..x8 van, tehát kezdetben 8 klaszter létezik az 1. szinten. Tegyük fel, hogy az x1 és x2 pontok 2. szintű klaszterbe egyesülnek, majd a 8. szintig ugyanazon a klaszterön maradnak.
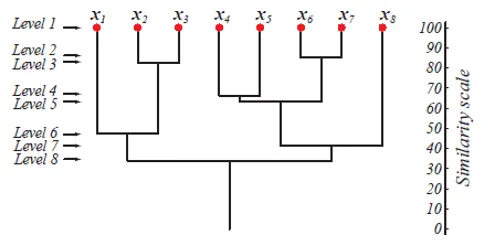
A fenti ábra az agglomerációs klaszterezési megközelítés dendrogramjának bemutatását mutatja 8 adatpontnál, valamint az egyes szintekhez tartozó hasonlósági skálát.
A klaszterek szintje elképzelést ad arról, hogy a klaszterek adatpontjai milyen hasonlóak. Mint az 1. ábrán látható, az adatpontok korábban egy klaszterbe egyesülnek, hasonlóak. Tehát a 2. szintű fürtön belüli adatpontok (pl. X2 és x3) hasonlóak, mint a 6. szintű fürt adatpontjai (pl. X1 és x2).
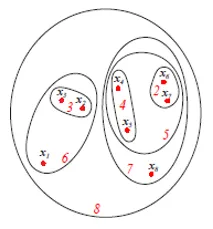
A fenti ábra a fenti 8 adatpont agglomerációs klaszterezési megközelítésének Set vagy Venn diagramját mutatja. Mind a dendrogramok, mind a halmaz reprezentációk felhasználhatók a klaszterezéshez. Azonban a dendrogram általában előnyösebb eszköz-ábrázolás nem képes mennyiségileg ábrázolni a klaszter hasonlóságait.
A hierarchikus klaszterezési algoritmus lépései
Kövesse az alábbi lépéseket a hierarchikus klaszterezési algoritmushoz:
1. Algoritmus
Agglomerációs hierarchikus klaszterezési algoritmus
- Inicializálás kezdete c, c1 = n, Di = (xi), i = 1, …, n '
- Csináld c1 = c1 - 1
- Keresse meg a legközelebbi klasztereket, mondjuk, Di és Dj
- Merge Di és Dj
- C = c1-ig
- Visszaadja a c klasztereket
- vég
Ez az algoritmus kezdetben n klaszterrel kezdődik, ahol minden adatpont egy klaszter. Minden iterációval a klaszterek száma 1-rel csökken, mivel a 2 legközelebbi klaszter egyesül. Ez a folyamat addig folytatódik, amíg a klaszterek száma az előre meghatározott c értékre csökken.
Hogyan lehet eldönteni, mely klaszterek vannak a közelben?
Ezt több távolságmérővel definiálják, amelyek a következők:
- A klaszterek közötti minimális távolság dmin (Di, Dj). Egyedülálló.
- A klaszterek közötti legnagyobb távolság dmax (Di, Dj). Hasznos teljes.
- A klaszterek közötti átlagos távolság davg (Di, Dj).
Mi az egyszeres és teljes összeköttetés?
- Ha dmin (di, dj) -et használunk a két klaszter közötti távolság megkeresésére, és az algoritmus akkor fejeződik be, ha a legközelebbi klaszterek közötti távolság meghaladja a küszöböt, akkor az algoritmust egyetlen összekapcsolási algoritmusnak nevezzük.
- Ha a dmax-t (Di, Dj) használják a két klaszter közötti távolság megkeresésére, és az algoritmus akkor fejeződik be, ha a legközelebbi klaszterek közötti távolság meghaladja a küszöböt, akkor az algoritmust teljes összekapcsolási algoritmussal hívják.
- Tekintsük az egyes adatpontokat egy gráf csomópontjaként. Két adatpont között él van, ha ugyanabba a fürtbe tartoznak. Két legközelebbi klaszter egyesítésekor egy él kerül hozzáadásra. Egyszeres kapcsolatnak hívják, mert létezik egyedi út az egyik csomóponttól a másikig.
- A teljes kapcsolási algoritmus két klasztert egyesít azáltal, hogy minimalizálja a távolságot a két legtávolabbi pont között.
- Egyetlen kapcsolódási algoritmus átfogó fát hoz létre. Ez az algoritmus azonban érzékeny a zajra. A teljes kapcsolási algoritmus teljes grafikát hoz létre.
Mi az algoritmus időbeli összetettsége?
Tegyük fel, hogy n mintázatunk van a d-dimenziós térben, és a dmin (Di, Dj) értékét használjuk c klaszterek létrehozására. Ki kell számítanunk n (n - 1) pontok közötti távolságot - amelyek mindegyike O (d 2 ) számítás - és az eredményeket egy pontok közötti távolságtáblázatba kell helyezni. A tér komplexitása O (n 2 ). A minimális távolságpár megkereséséhez (az első egyesítéshez) megköveteli, hogy lépjünk át a teljes listán, megtartva a legkisebb távolság indexét.
Így az első agglomerációs lépésnél a bonyolultság O (n (n - 1) (d2 + 1)) = O (n 2 d 2 ). Egy másik önkényes agglomerációs lépéshez (azaz c1-től c1-1-ig) csak átlépünk az n (n - 1) - c1 „fel nem használt” távolságra a listában, és megtaláljuk a legkisebbet, amelyre x és x 'tartozik a különböző klaszterekben . Ez ismét O (n (n − 1) -c1). A teljes idő bonyolultsága tehát O (cn 2 d 2 ), és tipikus körülmények között n >> c.
2. Megjelenítés
Miután az adatokat klaszterekre osztották, jó gyakorlat a klaszterek megjelenítése, hogy megértsék, hogyan néz ki a csoportosítás. Ennek a nagy dimenziós adatoknak a megjelenítése azonban nehéz. Ezért a fő alkotóelem-elemzést (PCA) használjuk a megjelenítéshez. A PCA után megkapjuk az adatpontokat az alacsony dimenziós térben (általában 2D vagy 3D), amelyeket ábrázolhatunk a csoportosításhoz.
Megjegyzés: A nagy dimenzió sok funkciót jelent, és nem sok adatpontot.3. Értékelés
A klaszterek értékelésének egyik módszere az, hogy a klaszterek közötti pontok távolságának (klaszterek közötti távolságnak) sokkal nagyobbnak kell lennie, mint a klaszterben lévő pontok távolságának (klaszterön belüli távolság).
Következtetés
Az alábbiakban bemutatjuk néhány kulcsfontosságú elvitelre:
- A hierarchikus klaszterezési algoritmust az adatok beágyazott mintáinak megkeresésére használják
- A hierarchikus csoportosítás kétféle: osztó és agglomerációs
- A dendrogram és a set / Venn diagram használható a reprezentációhoz
- Az egyszeres összeköttetés két klasztert egyesít, minimálisra csökkentve a közöttük lévő távolságot. Ez egy átfogó
- A teljes kapcsolat két klasztert egyesít azáltal, hogy minimalizálja a maximális távolságot. Teljes gráfot képez.
- A hierarchikus klaszterezési algoritmus teljes időbeli összetettsége O (cn 2 d 2 ), ahol c az előre meghatározott klaszterek száma, n a minták száma és d az n mintázat d-dimenziós térje.
Ajánlott cikkek
Ez egy útmutató a Hierarchical Clustering algoritmushoz. Itt tárgyaljuk a hierarchikus klaszterezési algoritmusok típusait és lépéseit. A következő cikkeket is megnézheti további információkért -
- Hierarchikus klaszterelemzés
- Hierarchikus csoportosítás R '-ben
- Klaszterezési algoritmus
- Mi a klaszterezés az adatbányászatban?
- Hierarchikus csoportosítás | Agglomerációs és megosztó csoportosulás
- C ++ algoritmus | Példák a C ++ algoritmusra