
Excel SIN funkció (Tartalomjegyzék)
- SIN függvény Excelben
- Hogyan lehet használni a SIN függvényt az Excelben?
SIN függvény Excelben
A számítás képessége nem terjed ki a matematika teljes területére. Ez egy alszakasz, bár alkalmazása szempontjából létfontosságú. Az elmúlt években ez volt a korlátozó tényező, kivéve a nagyon elismert és legtehetségesebben tehetséges „emberi számológépeket”, mint például Shakuntala Devi. A számítógépek azonban most lehetővé teszik, hogy az egész matematikát intellektuálisabbá tegye. A matematika fogalma és tétele sokkal hangsúlyosabb, mint valaha.
Az Excel nagyon ügyes a matematikai modellek sokaságának kezelésében, matematikai és logikai funkciók hatalmas gyűjteményével van felszerelve, hogy támogassa a különféle műveleteket. Teljes trigonometrikus funkciókkal rendelkezik, amelyek segítenek nekünk, amikor a trigonometria világába kerülünk.
Tehát a Sine trigonometrikus függvény megoldásához biztosítja a SIN függvényt . Ez egy alapvető trigonometrikus függvény, de különösen hasznos, ha a gyártási, navigációs vagy kommunikációs iparban dolgozik. Fontos megjegyezni, hogy az Excel radiánokat, nem fokokat használ a trigonometrikus kifejezés kiszámításához. Ennek két módja van:
- Emlékezzünk arra, hogy π = 180 °. Tehát, ha a szög fokban van, szorozzuk meg π / 180 ° -kal, hogy radiánokká alakítsuk. Excelben ezt a konverziót PI () / 180-nak lehet írni. Például, ha 60 ° -ot radiánussá alakítunk, akkor az Excel kifejezés 60 * PI () / 180 lenne, amely egyenlő 1, 0472 radiánnal.
- Az Excel fel van szerelve egy nagyon hasznos eszközzel is, amelyet RADIANS-nak hívnak. Érvként elfogad egy szöget, amelyben a szög azokra a fokokra vonatkozik, amelyeket radiánussá kell átalakítani. Vegyük például, ha a 210 ° radiánussá történő átalakításához használt kifejezés „RADIANS (210)”, és 66519 radiánra értékei.
Ezzel szemben a DEGREES segédprogram ugyanolyan fontos. Ez a funkció felhasználható a RADIANS függvény pontosan ellentétes irányába, a radiánok fokokra konvertálásával. Például a DEGREES (PI () / 2) 90-et értékeli.
Hogyan lehet használni a SIN függvényt az Excelben?
Megértjük, hogyan lehet az SIN függvényt használni az Excelben néhány példa és az SIN függvény valós életbeli illusztrációi segítségével.
Itt letöltheti ezt a SIN Function Excel sablont - SIN Function Excel TemplateSIN függvény az Excelben - 1. példa
A szinuszérték kiszámítása az Excel SIN függvényével
Egy adott szám szinuszának megállapításához először = SIN () kell írni egy adott cellába.

Amint az a fenti képernyőképről látható, az Excel SIN funkciója számot ír elő bemenetként. Ez a szám általában egy értéket mutat radiánban.
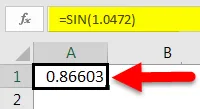
Tehát ebben az esetben a következőt fogjuk írni: = = SIN (1.0472), ahol 1.0472 a radián ekvivalens 60 fok.
Miután ezt megtettük, 60 fokos SIN értéket kapunk.
SIN függvény az Excelben - 2. példa
A szinuszérték kiszámítása az Excel SIN és RADIAN függvényével
Most nézzük meg, hogyan tudjuk eredményesebben használni a SIN-et, abban az esetben, ha nem tudjuk a fok fokának pontos sugárértékét.
A RÁDIÁNOK () segítségével megtudjuk a sugárérték értékét, amelyet argumentumként adunk át a SIN függvényhez.
Tehát a SIN korábbi verziójával kezdjük ():

Ezután átadjuk a RADIANS (60) érvként a SIN függvényt, ahol 60 az érték fokban.

Amint a fenti példából láthatjuk, a RADIANS () elfogad egy értéket fokban. Tehát a 60 értéket átadjuk a RADIANS () -nek.

Ezután nyomja meg az Enter billentyűt . Ez a következő eredményt adja.

Tehát látjuk, hogy az eredmény megegyezik az első példával.
SIN függvény az Excelben - 3. példa
A szinuszérték kiszámítása az Excel SIN és PI függvényével
Van még egy módja annak, hogy egy fokértéket radiánokká konvertáljunk a SIN függvényben történő felhasználás céljából. Az iskolában töltött időnkről arra emlékezünk, hogy π = 180 °. Tehát, ha a szög fokban van, szorozzuk meg π / 180 ° -kal, hogy radiánokká alakítsuk. Excelben ezt a konverziót PI () / 180-nak lehet írni. Például, ha 60 ° -ot radiánussá alakítunk, akkor az Excel kifejezés 60 * PI () / 180 lenne, amely egyenlő 1, 0472 radiánnal.
Nézzük meg, hogyan működik ez:
Először a SIN függvény megírásával kezdjük, a fentiek szerint.

Ezután közvetlenül átadjuk a 60 ° -ot argumentumként a SIN függvényhez. De ez nem adna nekünk a megfelelő sugárirányú 60 fokot. Ennélfogva a 60-at megszorozzuk PI () / 180-tal.

Ez a következő eredményt fogja kapni:
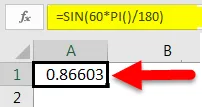
Mint láthatjuk, ez megegyezik a fenti példákkal.
SIN függvény Excelben - 4. példa
Nézzük meg egy másik példát, amely bemutatja a SIN függvény eredményeit a különféle értékekre.

A fenti táblázatban bemutatott eredmények magyarázata:
1. és 2. eset:
3, 14 a Pi értéke, és mindkét módszerrel felhasználhatjuk a 0 értékének megszerzését. Ez alapvetően azt jelenti, hogy a radianok SIN értéke 0 .
3. és 4. eset:
A Radian és a Pi / 180 értéke matematikában azonos, ezért a SIN függvény ugyanazt az értéket adja. Mindkét példa 30 fokos SIN-t jelent, amely 0, 5 értéket ad.
5. és 6. eset:
SIN 45 = 0, 85 a 45 radián SIN értéke, amely alapértelmezés szerint az excel az összes szöget sugárban veszi, és nem fokot. Fokozatba való konvertálásához használhatjuk a radián függvényt és 45 fokos SIN értéket kapunk, amint az az utolsó sorban látható. azaz SIN (RÁDIÁNOK (45)) = 0, 707 vagy 0, 71
SIN függvény az Excelben - 5. példa
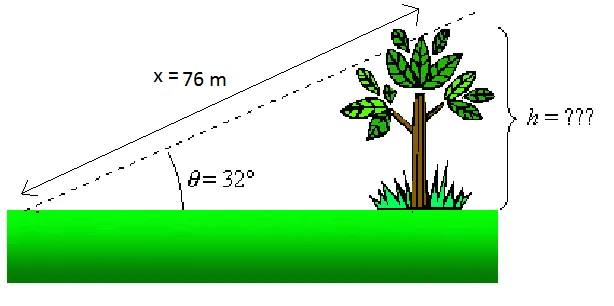
Tegyük fel például, hogy szeretnénk tudni a fa magasságát a fenti ábrán. Tudjuk, hogy ha 76 m-re állunk a fa tetejétől (x = 76 m), a látóvonal a fa tetejéhez a horizonthoz viszonyítva 32 ° (θ = 32 °). Tudjuk:
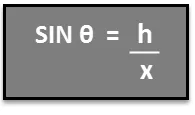
Ezért a h fa magasságának feloldására h = x SIN θ értéket találunk .

A SIN függvénynek csak egy argumentuma van, amely egy szám. A SIN kiszámításához számra van szükség. Ezért elengedhetetlen, hogy fokokat radiánban számra konvertáljunk, mielőtt megállapítanánk annak szinuszát.
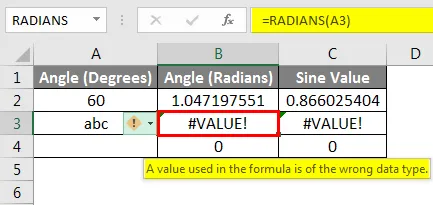
A SIN funkció megjeleníti a #VALUE! hiba, ha a függvény argumentumként használt hivatkozás egy szöveges adatokat tartalmazó cellára mutat. Az alább bemutatott példában a harmadik sor cellahivatkozása a szövegcímkére mutat, szögben (fokban) . Mivel a SIN funkciók csak egy számot támogatnak argumentumként, a SIN hibát fog értékelni, ebben az esetben #VALUE! . Ha a cella üres cellára mutat, akkor a függvény az alábbi példa szerint nulla értéket ad vissza. Az Excel trigonometrikus függvényei az üres cellákat nullának értelmezik, és a nulla radián szinusza nulla.
SIN függvény az Excelben - 6. példa
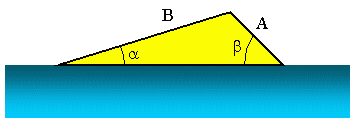
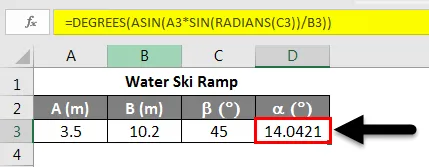
Tegyük fel, hogy szeretnénk megtudni a vízisí rámpájának indulási szögét, ahogy az a fenti ábrán látható. Tudjuk, hogy A = 3, 5 m, B = 10, 2 m és b = 45, 0 °. Most, hogy megtaláljuk a, használhatjuk a szinusz törvényét. Ebben a forgatókönyvben a következőképpen lehet írni:
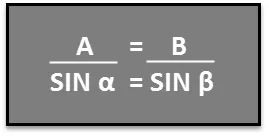
Ezt az egyenletet úgy alakíthatjuk át, hogy:
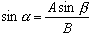
Az ív vagy inverz szinusz segítségével megtudhatjuk az α szöget. Az alább látható egyenlet alkalmazásával.

7. példa
A végső trigonometrikus példánkban az Excel segítségével fogjuk megvizsgálni a trigonometrikus identitást:
sin²θ + cos²θ = 1
Vegye figyelembe, hogy az alábbi képernyőképen ez az identitás igaz, ha θ radiánban és fokban egyaránt megadott.

Vegye figyelembe, hogy az the szög mértékegysége nem más, mint a cellák. Ha a számokat és az egységeket ugyanabba a cellába helyezzük, az Excel nem fogja tudni megkülönböztetni a számot a szövegtől, ezért nem tudjuk hivatkozni a cellákra az egyenletben való felhasználás céljából, és az #VALUE! hiba.
Dolgok, amikre emlékezni kell
- Ne feledje, hogy az SIN függvény alapértelmezés szerint a Radiannal működik.
- Konvertálja a számot a sugárban vagy a fokban szükséges módon, akár RADIANS, akár DEGREES funkcióval.
- Használhatja a PI () függvényt, hogy pontos eredményeket kapjon a SIN funkcióról, miközben π-vel dolgozik.
Ajánlott cikkek
Ez egy útmutató az Excel SIN funkciójához. Itt tárgyaltuk, hogyan lehet használni a SIN függvényt az Excelben, a gyakorlati példákkal és a letölthető Excel sablonnal együtt. Megnézheti más javasolt cikkeinket -
- Az matematika fontos funkciói az Excelben (egyszerű)
- Útmutató a képlet elválasztásához az Excelben
- Fontos fejlett Excel képletek és funkciók
- Az Excel képletek Cheat Sheet