
Bevezetés az egyesítésbe a JavaScript-ben
A rendezési algoritmusok nagyon fontosak a számítástechnikában. A rendezés eredménye a lista elemeinek bizonyos sorrendbe rendezése (növekvő vagy csökkenő). Az Egyesítés a JavaScript-ben az egyik leghatékonyabb rendezési algoritmus, amely a megosztás és a hódítás fogalmán alapul. Ahogy a neve is sugallja, előbb ossza meg a nagyobb problémát kisebb problémákra, mint oldja meg a kisebb problémákat a nagyobb probléma megoldása érdekében. Fogalmi szempontból a Merge sort két alapvető algoritmus kombinációja, az úgynevezett MERGE és MERGE_SORT.
amely a következőképpen működik:
- Ossza meg a válogatott listát n számú egyelemű allistára (n a válogatott listában szereplő összes elem száma).
- Az allistákat ismételten egyesítjük rendezett allistákba, amíg csak egy rendezett lista lesz.
A Merge Sort végrehajtása a JavaScript-ben
A MERGE algoritmus követi az eljárást, amikor két rendezett listát egy rendezett listává kombinálnak.
Példa: Tegyük fel, hogy két lista létezik, azaz 1. lista (1, 5, 3) és a 2. lista (7, 2, 9).
1. Először rendezze el mindkét listát.
Most meglátjuk és alkalmazzuk az E technikát.
2. Ezután elkészítjük az x + y méretű új listát, ahol x az 1. listában szereplő elemek száma és y a 2. listában szereplő elemek száma.

Esetünkben x = 3 és y = 3, tehát x + y = 6.
3. Most két mutatónk van.
Az első mutató az 1. lista első helyzetére mutat, és a második mutató a 2. lista első helyzetére mutat.

4. Ezután összehasonlítjuk mindkét mutató értékét. A kisebb értékű mutatót, másolja át az elemet a 3. listába, és mozgassa az egérmutatót jobb oldalra a kisebb értékű és az ennek eredményeként létrejövő lista számára (azaz az 1. és a 3. lista).

5. Hasonlóképpen hajtsa végre újra és újra a 4. lépést.

További út…
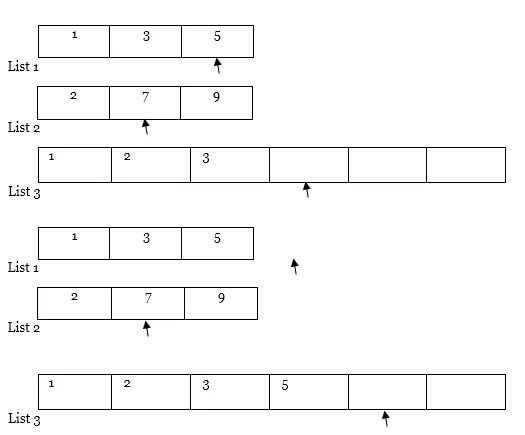
Megjegyzés : Ha az egyik lista (azaz az 1. vagy a 2. lista) teljes mértékben áthalad, mint az eset, akkor másolja a másik lista teljes tartalmát a mutatóról az eredménylistára (azaz a 3. listára) az alábbiak szerint.

pszeudókód
Function merge (sublist1, sublist2) (
Create var for result list
While sublist1 length > 0 and sublist2 length > 0
If sublist1(0) < sublist2(0) Copy the sublist1 pointer value to result list and Shift pointer of sublist1 to right
else
Copy the sublist2 pointer value to result list and Shift pointer of sublist2 to right
Return concat sublist1 or sublist2 (depending if node1 is empty or not)
A MERGE_SORT algoritmus megosztja az adott válogatott listát a minimális méretre, majd felhívja a MERGE algoritmust, hogy a listát az új rendezett listává egyesítse.
pszeudókód
function mergeSort(list) (
If list length < 2
Return list
Create var for middle index of list
Create var for left index of list
Create var for right index of list
Recursively call mergeSort function
)
Példa
Itt az alulról lefelé haladó Merge Sort rendezést követjük. A tetején kezdődik, és lefelé halad, minden rekurzív fordulással ugyanazt a kérdést kell feltenni: „Mit kell tenni a lista rendezéséhez?”, És a válasz: „Osszuk fel a listát két részre, rekurzív hívást kezdeményezünk és egyesítjük a eredmények".
Kód a Javascript-ben
// Split the list into halves and merge them recursively
function mergeSort (list) (
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
var mid = Math.floor(list.length / 2);
var left = mergeSort(list.slice(0, mid));
var right = mergeSort(list.slice(mid));
return merge(left, right);
)
// compare the lists element by element and return the concatenated resultList
function merge (sublist1, sublist2) (
var resultList = ();
while (sublist1.length > 0 && sublist2.length > 0)
resultList.push(sublist1(0) < sublist2(0)? sublist1.shift() : sublist2.shift());
return resultList.concat(sublist1.length? sublist1 : sublist2);
)
const list = (6, 5, 3, 1, 8, 7, 2, 4, 2, 5, 1, 2, 3) console.log(mergeSort(list)) //( 1, 1, 2, 2, 2, 3, 3, 4, 5, 5, 6, 7, 8 )
Az egyesítési sorrend fő funkciója az adott listát kisebb listákra osztja a rekurzív hívás minden iterációja során. Ne felejtse el, hogy a rekurzióhoz szükség van az alapfeltételre a végtelen rekurzió elkerülése érdekében. Esetünkben:
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
Miután beállítottuk a rekurzió alapfeltételét, meghatározzuk a középső indexet, amellyel az adott listát balra és jobbra oszthatjuk, ahogyan azt a példadiagram fent láthatja. Ezután össze kell vonnunk a bal és a jobb allistát, amelyeket most megnézünk. A fenti egyesítési funkcióban meg kell győződnünk arról, hogy a bal al- és a jobb al- lista. Ahogy ezt megtesszük, egy ideiglenes hurkot használunk. A rövid időn belül a bal oldali allistában és a jobb allistában szereplő elemet egyenként hasonlítjuk össze. Kihúzhatjuk az eredménylistába, és ennek megfelelően mozgathatjuk a kurzort a bal és a jobb allistához. Végül össze kell kötnünk az eredménylistát. Ez nagyon fontos! Ha itt nem végezzük el ezt az utolsó lépést, akkor a végén nem lesz teljes az elemek listája, mivel a loop ciklus akkor sikertelen, ha a két mutató valamelyike eléri a végét.
Kimenet:

A Merge Sort tulajdonságai
- Az egyesítés rendezése stabil, mivel a tömb ugyanaz az eleme megtartja eredeti helyzetüket egymáshoz viszonyítva.
- Az egyesítés nem "a helyén", mivel az egyesítés során létrehozza a teljes lista másolatát. Emiatt ennek az algoritmusnak a tér bonyolultsága (O (n)) valójában nagyobb, mint másoké, és nem szabad használni olyan összetett problémákban, ahol prémium a hely.
- Az egyesítés általános időbeli összetettsége O (nLogn). Hatékonyabb, mivel a legrosszabb esetben is, a futási idő O (nlogn).
Következtetés
Az egyesítési sorrendben a legjobb, a legrosszabb és az átlagos esetek komplexitása azonos, ami hatékonyabb algoritmust eredményez. Gyorsabban működik, mint más válogatási technikák. Az egyesítés sort bármilyen méretű fájlra alkalmazható. Nagyon párhuzamosítható az osztás és hódítás módszer alkalmazásának köszönhetően. A számítástechnika alapjainak fejlesztése érdekében tanácsos alaposan megérteni a különféle rendezési algoritmusokat.
Ajánlott cikk
Ez egy útmutató a Merge Sort számára a JavaScripten. Itt tárgyaljuk az Összevonás rendezése bevezetését a JavaScript-ben és a megvalósítást, valamint a Tulajdonságokat. A további javasolt cikkeken keresztül további információkat is megtudhat -
- JavaScript matematikai funkciók
- Bevezetés a JavaScript-be
- A legjobb Javascript keretek
- JavaScript eszközök
- A 6 legnépszerűbb rendezési algoritmus a JavaScript-ben