
Bevezetés az ANOVA-ba R
A következő, az R-ben szereplő ANOVA cikk felvázolja a különböző csoportok középértékének összehasonlítását. A varianciaanalízis (ANOVA) nagyon gyakori módszer a különféle csoportok középértékének összehasonlítására. Az ANOVA modellt alkalmazzák a hipotézis tesztelésére, ahol bizonyos feltevéseket vagy paramétereket generálnak egy populációra, és a statisztikai módszert használják annak meghatározására, hogy a hipotézis igaz vagy hamis.
A hipotézist a kutató feltételezéséből és a lakossággal kapcsolatban rendelkezésre álló információból nyerjük. Az ANOVA-t varianciaanalízisnek nevezik, és azt a hipotézis tesztelésére használják, ahol meg kell mérni egy változó átlagát több független csoportban.
Például egy laboratóriumban az elhízás szempontjából új gyógyszer tanulmányozására vagy feltalálására a kutatók összehasonlítják a kísérleti és a standard kezelés eredményét. Az elhízási tanulmányban értékes eredmények nyerhetők, amikor a lakosság átlagos elhízási aránya összehasonlítható különféle korcsoportokban. Ebben az esetben meg akarjuk figyelni az átlagos elhízás mértékét a különféle korcsoportok között, például az életkor (5-18 év), (19, 35 év) és (36-50 év). Az ANOVA módszert alkalmazzák, mivel több mint két csoport független. Az ANOVA módszert használják a független csoportok átlagos elhízásának összehasonlítására. Az aov () függvényt használjuk, és a szintaxist aov (képlet, data = dataframe) Ebben a cikkben megismerjük az ANOVA modellt, és tovább tárgyaljuk az egyirányú és kétirányú ANOVA modellt, valamint a példákat.
Miért az ANOVA?
- Ez a módszer a hipotézis megválaszolására szolgál, több adatcsoport elemzése közben. Számos statisztikai megközelítés létezik, azonban az ANOVA in R alkalmazandó abban az esetben, ha összehasonlítást több mint két független csoportra kell elvégezni, mint az előző példánkban három különböző korcsoportra.
- Az ANOVA technika a független csoportok átlagát méri a kutatók számára a hipotézis eredményének biztosítása érdekében. A pontos eredmények elérése érdekében figyelembe kell venni a minta átlagát, a minta méretét és az egyes csoportoktól való szórást.
- Az összehasonlításhoz mindhárom csoportra külön-külön megfigyelhető az átlag. Ennek a megközelítésnek azonban vannak korlátozásai, és helytelennek bizonyulhat, mivel ez a három összehasonlítás nem veszi figyelembe az összes adatot, így az 1. típusú hibához vezethet. R feladatot nyújt az ANOVA elemzés elvégzésére a független adatcsoportok közötti variabilitás vizsgálatára. Az ANOVA elemzés elvégzésének öt lépése van. Az első szakaszban az adatok csv formátumban vannak elrendezve, és az oszlop minden változóhoz előállítva. Az egyik oszlop függő változó lenne, a többi pedig a független változó. A második szakaszban az adatokat R stúdióban olvassa és megfelelő módon megnevezi. A harmadik szakaszban egy adatkészletet csatolunk az egyes változókhoz, és a memória elolvassa. Végül meghatározzuk és elemezzük az R-ben lévő ANOVA-t. Az alábbiakban néhány esettanulmány-példát mutattam be, amelyekben az ANOVA technikákat kell használni.
- Hat rovarirtó szert teszteltünk mindegyik 12 mezőn, és a kutatók megszámolták az egyes területeken megmaradt hibák számát. Most a gazdálkodóknak tudniuk kell, hogy van-e különbség az rovarirtó szereknek, és ha igen, melyiket használják a legjobban. Erre a kérdésre az aov () függvény segítségével válaszolsz, hogy végrehajts egy ANOVA-t.
- Ötven beteg részesült az öt koleszterinszint-csökkentő gyógyszerkezelés egyikében (trt). A kezelési körülmények közül három ugyanazt a gyógyszert tartalmazta, mint napi egyszeri 20 mg-os adaggal (egyszer) 10 mg-os, napi kétszer (kétszer), 5 mg-os, napi négyszer (négyszer). A fennmaradó két állapot (drugD és drugE) versengő gyógyszereket képviselt. Melyik gyógyszeres kezelés eredményezi a legnagyobb koleszterinszintet (választ)?
ANOVA egyirányú
- Az egyirányú módszer az ANOVA egyik alapvető technikája, amelyben varianciaanalízist alkalmaznak, és összehasonlítják a több populációs csoport átlagát.
- Az egyirányú ANOVA megkapta a nevét, mivel rendelkezésre állnak egyirányú minősített adatok. Egyirányú ANOVA egyetlen függő változó és egy vagy több független változó is elérhető.
- Például az ANOVA technikát végrehajtjuk a koleszterin adatkészletre. Az adatkészlet két trt változóból áll (amelyek 5 különböző szint kezelései) és válaszváltozóból állnak. Független változó - drogkezelési csoportok, függő változó - 2 vagy több csoport ANOVA átlaga. Ezekből az eredményekből megerősítheti, hogy az 5 mg-os adagok napi 4-szer történő bevétele jobb volt, mint a napi egyszeri 20 mg-os adag bevétele. A D gyógyszer jobb hatást mutat, mint az E gyógyszer
A D gyógyszer jobb eredményeket nyújt, ha 20 mg-os dózisban veszik be az E drogot
A koleszterin adatkészletet használja a multcomp csomagbaninstall.packages('multcomp')
library(multcomp)
str(cholesterol)
attach(cholesterol)
aov_model <- aov(response ~ trt)
A kezelés ANOVA F-tesztje (trt) szignifikáns (p <.0001), bizonyítékot szolgáltatva arra, hogy az öt kezelés
# nem egyformán hatékony.
összefoglaló (aov_model)
Detach (koleszterin)

A plotmeans () függvény a gplots csomagban felhasználható az átlagcsoport és azok konfidencia-intervallumainak grafikonjának elkészítésére. Ez egyértelműen mutatja a kezelési különbségeketinstall.packages('gplots')
library(gplots)
plotmeans(response ~ trt, xlab="Treatment", ylab="Response",
main="Mean Plot\nwith 95% CI")
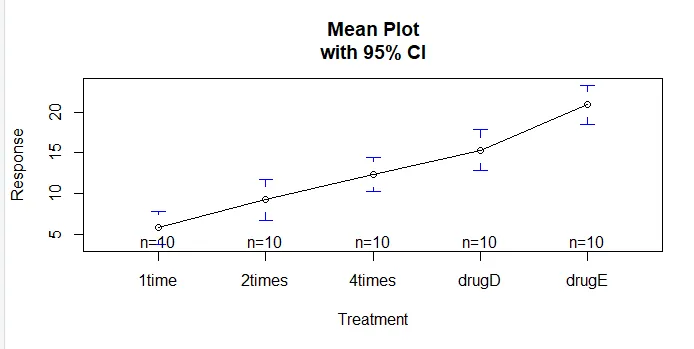
Vizsgáljuk meg a TukeyHSD () kimenetét a csoport átlagok közötti páros különbségek szempontjából
TukeyHSD (aov_model)
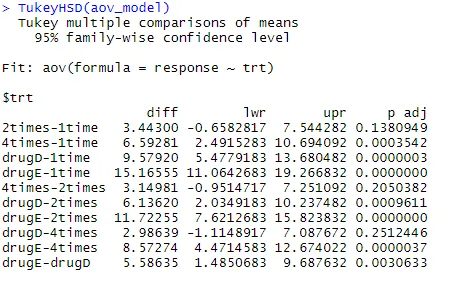
Az átlagos koleszterinszint csökkentés egyszer és kétszer nem különbözik szignifikánsan egymástól (p = 0, 138), míg az egyszeri és négyszeres különbség szignifikánsan eltér (p <0, 001).
par (mar = c (5, 8, 4, 2)) # a bal oldali margó diagramjának növelése (TukeyHSD (aov_model), las = 2)
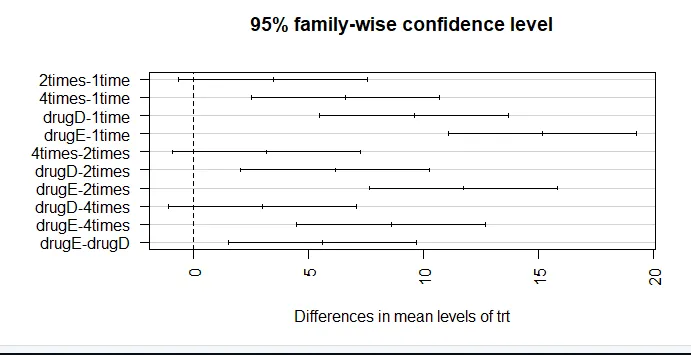
Az eredményekbe vetett bizalom attól függ, hogy az adatai milyen mértékben felelnek meg a statisztikai tesztek alapjául szolgáló feltételezéseknek. Az egyirányú ANOVA esetén a függő változót feltételezzük, hogy normálisan eloszlott és egyenlő varianciával rendelkezik az egyes csoportokban. Használhat egy QQ diagramot a normalitási feltételezési könyvtár (autó) értékeléséhez.
QQ diagram (lm (válasz ~ trt, adatok = koleszterin), szimulál = IGAZ, main = ”QQ plot”, címkék = FALSE)
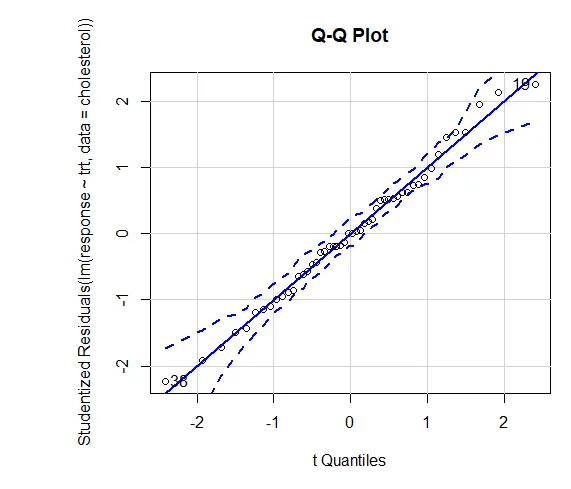
Pontozott vonal = 95% -os megbízhatósági boríték, ami arra utal, hogy a normalitási feltételezés meglehetősen jól teljesült. ANOVA azt feltételezi, hogy a varianciák csoportokon vagy mintákon azonosak. A Bartlett-teszt felhasználható a feltételezés igazolására
bartlett.test (válasz ~ trt, adatok = koleszterin). Bartlett-teszt azt mutatja, hogy az öt csoport varianciái nem különböznek szignifikánsan (p = 0, 97).
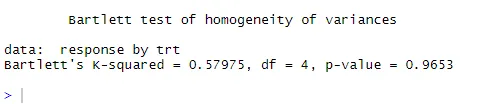
Az ANOVA érzékeny a túlmutatókkal szembeni tesztre is, az outlierTest () függvényt használva az autócsomagban. Lehet, hogy nem kell ezt a csomagot futtatnia az autókönyvtár frissítéséhez.update.packages(checkBuilt = TRUE)
install.packages("car", dependencies = TRUE)
library(car)
outlierTest(aov_model)
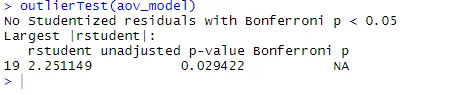
A kimeneti adatok alapján láthatjuk, hogy a koleszterin-adatokban nincs utalás (NA akkor fordul elő, ha p> 1). A QQ-diagramot, a Bartlett-tesztet és a külső tesztet együttesen véve úgy tűnik, hogy az adatok elég jól megfelelnek az ANOVA modellnek.
Kétirányú Anova
Egy másik változót adunk a kétirányú ANOVA teszthez. Ha két független változó létezik, akkor kétirányú ANOVA-t kell használnunk, nem pedig az egyirányú ANOVA-technikát, amelyet az előző esetben alkalmaztak, ahol volt egy folyamatos függő változónk és egynél több független változónk. A kétirányú ANOVA ellenőrzéséhez többféle feltételezést kell teljesíteni.
- A független megfigyelések rendelkezésre állása
- A megfigyeléseket általában szét kell osztani
- A szórásnak megfigyelésben azonosnak kell lennie
- A távoli személyeknek nem szabad jelen lenniük
- Független hibák
A kétirányú ANOVA ellenőrzéséhez egy másik BP nevű változót adunk az adatkészlethez. A változó a vérnyomás arányát jelzi a betegekben. Szeretnénk ellenőrizni, hogy van-e statisztikai különbség a BP és a betegeknek adott adag között.
df <- read.csv (“file.csv”)
df
anova_two_way <- aov (válasz ~ trt + BP, data = df)
összefoglaló (anova_two_way)
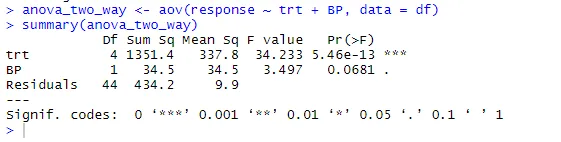
A kimenet alapján arra lehet következtetni, hogy mind a trt, mind a BP statisztikailag különbözik a 0-tól. Ezért a Null hipotézist el lehet utasítani.
Az ANOVA előnyei R
Az ANOVA teszt meghatározza a két vagy több független csoport közötti átlagkülönbséget. Ez a módszer nagyon hasznos több elem elemzéséhez, amely nélkülözhetetlen a piaci elemzéshez. Az ANOVA teszt segítségével az adatokból betekintést nyerhetünk. Például egy termékfelmérés során, ahol több információt gyűjtöttek a felhasználótól, például bevásárló listákat, vásárlói kedveket és nemtetségeket. Az ANOVA teszt segít összehasonlítani a népességcsoportjait. A csoport lehet férfi vagy nő, vagy különféle korcsoportok. Az ANOVA technika segít megkülönböztetni a népesség különböző csoportjainak átlagértékeit, amelyek valóban különböznek egymástól.
Következtetés - ANOVA R
Az ANOVA az egyik leggyakrabban alkalmazott módszer a hipotézis teszteléséhez. Ebben a cikkben elvégeztük az ANOVA tesztet az ötven betegből álló adatkészlettel, akik koleszterinszint-csökkentő gyógyszeres kezelést kaptak, és tovább láttuk, hogy hogyan lehet kétutas ANOVA végrehajtani, ha rendelkezésre áll egy további független változó.
Ajánlott cikkek
Ez egy útmutató az ANOVA-hoz R.-ban. Itt egyirányú és kétirányú Anova-modellt tárgyalunk, valamint az ANOVA példáit és előnyeit. Megnézheti más javasolt cikkeinket -
- Regresszió vs ANOVA
- Mi az SPSS?
- Az eredmények értelmezése az ANOVA teszt segítségével
- Funkciók R-ben