Vektorok Matlabban A vektorművelet típusai példákkal

Bevezetés a Matlab vektorokba

A vektor egy zárt elemkészlet. A Matlabban szögletes zárójelek segítségével hozhatunk létre vektorokat. A vektorok a tömbök egy példája (egydimenziós tömb). kétféle módon reprezentálható sorvektorral és oszlopvektorral.

Sor vektor

Ez vízszintes elemkészlet. Ez szögletes zárójelben található. Minden elemet vesszővel vagy szóközzel választ el egymástól.

X = (4 7 8) vagy X = (4, 7, 8)

Oszlop vektor

Ez egy függőleges elemkészlet. Ez is szögletes zárójelben szerepel. Az oszlopvektorok létrehozásának kétféle módja van: először az egyes elemeket pontosvesszővel választják el, és egy másik módszer az, ha az elemeket a parancssor következő sorába írják.

X = (4; 6; 7) vagy

X = (4

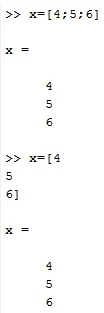
Vektoros műveletek

A vektor operátorokat nagyjából két kategóriába sorolják.

1. Számtani művelet

Vegyünk két x és y vektort x = (1 4 5 3) és y = (5 3 2 1) értékkel, különféle mûveleteket hajthatunk végre ezen a két x és y vektoron.

a. Szorzás: Ezt a funkciót arra használják, hogy a teljes vektort bármilyen aritmetikai értékkel megszorozzák.

Például:

mul = 3 * x

mul = 3 * (1 4 5 3)

mul = (3 12 15 9)

Szintaxis: variable name = arithmetic constant * vector name

b. Trigonometrikus függvény: Bármely trigonometrikus függvény alkalmazható vektorszerű sin, cos, tan, cosec, sec stb.

Tri példa = cos (x)

A válasz: 0, 54–0, 65 0, 28 –0, 99

Szintaxis: variable name = trigonometric function name ( vector name )

Összeg: Ez a teljes elem összes (hozzáadását) mutatja egy vektorban.

Példa

x = (1 4 5 3)

Összesen = összeg (x)

A teljes teljesítmény = 13

Szintaxis: variable name = = sum ( vector name )

c. Hossz: Megmutatja az egyes vektorok hosszát, tegyünk egy vektort p = (9 7 5 3 1 9 7 5 3 1)

Példa

p = (9 7 5 3 1 9 7 5 3 1)

Len = hosszúság (p)

A kimenet Len = 10

d. Vektorok hozzáadása: Két vagy több vektor hozzáadása egyszerű művelet a Matlabban, vegyük figyelembe két p és q vektorot.

P = (4 6 3 2) és q = (5 7 9 1)

Add = p + q

A kimenet hozzáadása = (9 13 12 3)

Szintaxis: vector name operator ( + ) vector name

Hasonló módon kivonhatjuk a kivonást is, például sub = p - q

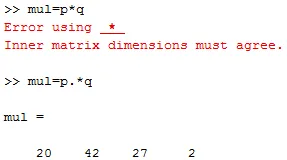
e. Vektorok szorzása: Ha két vektor szorzását akarjuk elvégezni, akkor az egyszerű szorzási operátor (*) nem fog működni. Ezért pont-operátort ('.') Kell hozzáadnunk a szorzó operátorhoz.

Példa:

P = (4 6 3 2) és q = (5 7 9 1)

mul = p. * q

a kimenet mul = (20 42 27 2)

Szintaxis: variable name = vector name dot operator multiplication operator vector name

Tegyük fel, hogy meg akarom találni egy adott vektor négyzetét, vagy csak a vektorral szeretném megszorozni.

Akkor a szintaxis squr = x lesz. 2

2. Relációs művelet

a. Egyenlő az operátorral : ez az operátor összehasonlítja az összes n elemet két vektorból, és kimenete nulla és egy alak.

Példa

m = (2 5 8)

És n = (5 5 3)

Mint tudjuk, az m vektorban és az n vektorban három elem létezik,

m == n

A fenti állítás eredménye 0 1 0 lesz, ami azt jelenti, hogy az első nem egyenlő, a második szám egyenlő, a harmadik nem pedig egyenlő. O jelentése hamis, 1 pedig igaz.

b. Kevesebb, mint operátor (<): Kevesebb, mint az operátor jelöli a „<” szimbólumot. összehasonlíthatunk egy adott mátrixot bármilyen aritmetikai állandóval vagy bármely más vektorral.

Példa

m = (3 2 4)

n = (1 1 1)

m <n

a kimenet 0 0 0 lesz, azaz minden szám nagyobb, mint n vektor.

és ha m <10

akkor a kimenet 1 1 1 lesz, azaz minden szám kevesebb, mint 10.

c. Nagyobb, mint operátor (>): Nagyobb, mint a kezelő szimbólummal ('>'). Össze lehet hasonlítani egy adott mátrixot bármilyen aritmetikai állandóval vagy bármilyen más vektorral.

Példa:

M = (3 2 4)

N = (1 1 1)

m> n

A kimenet 1 1 1 lesz, azaz minden érték nagyobb, mint az n vektor értéke.

Következtetés - Vektorok a Matlabban

A Matlabban különféle típusú vektorokat hozhatunk létre, ahol különféle műveleteket hajthatunk végre, mint például összeadás, kivonás, szorzás, négyzet, négyzetgyök, teljesítmény, skálázás, vektor szorzás, pont szorzat stb.

Ajánlott cikkek

Ez egy útmutató Matlabban található Vectors-hez. Itt tárgyaljuk a vektorműveletek típusait, amelyek magukban foglalják a számtani és a relációs műveletet, néhány példával együtt. A következő cikkeket is megnézheti további információkért -