
Különbség a Z pontszám és a T pontszám között
A Z pontszám a nyers adatok standard ponttá történő átalakítása, amikor az átváltás a népesség átlagán és a populáció szórása alapján történik. Ha rendelkezésre áll teljes adatkészlet, kiszámolhatjuk a Z-értéket. A Z pontszám a népesség átlagának a nyers pontszámból való kivonása, majd az eredményt elosztja a populáció szórásával. A T pontszám a nyers adatok átváltása a standard pontra, ha az átváltás a minta átlagán és a minta szórása alapján történik. Ha a népességre vonatkozó adatkészlet nem áll rendelkezésre, akkor a minta átlagának és a népesség szórásának kiszámításához ki kell vennie néhány mintaadatot.
Z pontszám
Normál eloszlás alatt, ahol teljes adatok állnak rendelkezésre, ez a távolság az átlagtól. A képlete a következő:
Z= (x-μ)/σ
Hol,
X = egyedi nyers adatok
μ = a népesség átlaga
σ = a lakosság szórása
T pontszám
A T pontszám az egyes standard szórások kivonása az egyéni átlagtól, majd az eredményt elosztjuk a minta szórásával, a teljes eredményt szorozva a minta méretével. A képlete a következő:
t = ((- μ)/s)*
= Minta átlag
μ = a népesség átlaga
s = Minta szórás
n = a minta mérete
Vegyünk egy példát, hogy ezt jobban megértsük:
Egy cikkben három alosztás található: I, II és III. Hagyja, hogy helyesen válaszoljon 25% -ot, azaz 75% -uk nem tudja helyesen válaszolni. Hasonlóképpen, tegyük 10% -ot és 20% -ot azon emberek számának megfelelően, akik helyesen válaszoltak a II. És a III. Szakaszra, tehát 90% és 80% találta meg a II. És a III. Szakaszt. Feltételezzük, hogy a három elem által mért képesség azonos és általában eloszlik,
Az osztály minden tanulójának pontszámát kiszámolják az 50-ös pontszámok átlaga és a szórás 10-ig. Kiszámolhatjuk a Z-pontszámot az 50-ös pontszámmal (50-50) / 10 = 0
Értelmezhetjük, hogy a hallgató pontszáma 0 távolság (standard eltérések egységében) az átlagtól, tehát a hallgató pontszámot kapott.
Ha a pontszám 60, a Z pontszám (60-50) / 10 = 1
Értelmezhetjük, hogy a hallgató átlag feletti pontszámot kapott - az átlag feletti 1 szórás távolsága.
A Z-pontszám és a T-pont közötti összehasonlítás (Infographics)
Az alábbiakban látható a 9 legmagasabb különbség a Z pontszám és a T pontszám között 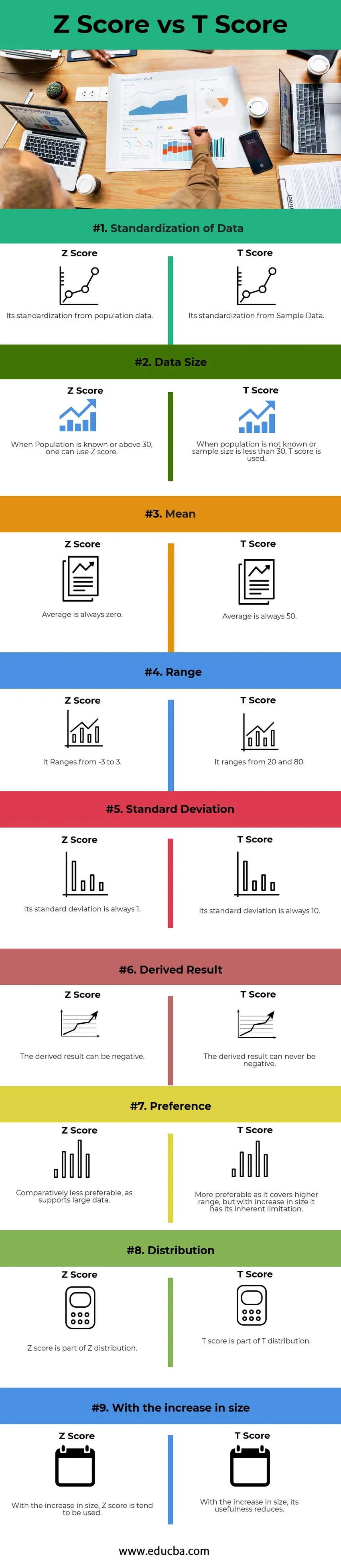
Főbb különbségek a Z pontszám és a T pontszám között
Beszéljünk néhány, a Z pontszám és a T pontszám közötti nagy különbségről
- A Z pontszám a népesség nyers adatainak vagy több mint 30 minta adatainak szabványosítása a normál pontszámhoz, míg a T pontszám a 30 adatnál kevesebb mintát tartalmazó adatok standardizálása
- A Z pontszám -3 és 3 között van, míg a T pontszám 20 és 80 között lehet.
- Az adatméret növekedésével az eloszlás általában Z-eloszlás. Mind a Z, mind a T pontszám eloszlás a normál eloszlás része, de méretük alapján különböznek egymástól
- Gyakorlatilag a Z-skálát széles körben használják a tőzsdei adatokban és egy társaság csődbe esésének ellenőrzésére, míg a t-értéket széles körben használják a csont ásványianyag-sűrűségének és a töréskockázat-becslések ellenőrzésére.
Z pontszám vs T pontszám összehasonlító táblázat
Nézzük meg a 9 legmagasabb összehasonlítást a Z pontszám és a T pontszám között
| Sr. Nem | Összehasonlítási pontok | Z pontszám | T pontszám |
| 1 | Az adatok szabványosítása | Szabványosítása a népesség adatai alapján | Szabványosítása a mintaadatokból |
| 2 | Adat mérete | Ha a lakosság ismert vagy 30 felett van, akkor a Z pontszámot lehet használni | Ha a populáció nem ismert vagy a minta mérete kevesebb, mint 30, akkor a T-pontszámot kell használni. |
| 3 | Átlagos | Az átlag mindig nulla. | Egy átlag mindig 50. |
| 4 | Hatótávolság | -3 és 3 közé esik. | 20 és 80 közé esik. |
| 5 | Szabványbeli eltérés | A szórása mindig 1 | A szórása mindig 10 |
| 6 | Származtatott eredmény | A származtatott eredmény negatív lehet | A származtatott eredmény soha nem lehet negatív |
| 7 | Előnyben | Viszonylag kevésbé előnyös, mivel támogatja a nagy adatokat | Még előnyösebb, mivel nagyobb tartományra terjed ki, de a méret növekedésével megvan a vele járó korlátozása |
| 8 | terjesztés | A Z pontszám a Z eloszlás része | A T pontszám a T eloszlás része |
| 9 | A méret növekedésével | A méret növekedésével a Z-pontszámot általában használják | A méret növekedésével csökken a hasznossága. |
Következtetés
Mind a Z, mind a T pontszám a hipotézis tesztelésének része a normál eloszlás mellett. Ha rendelkezik a különböző pontok mérési pontszámaival Z-pontok használatával, akkor megmondhatja, hogy a pontszámok hogyan kerülnek eloszlásukba. Akkor összehasonlíthatja őket. A pontszámok egységesítése széles körben alkalmazott eljárás a kutatás és a tervezés területén, mivel segítenek a különféle teszteredmények összehasonlításában. A pontszámok egységesítése, mielőtt összekapcsolnák, elősegíti a kutatót, hogy jobb és összehasonlítható eredményeket szerezzen.
Ajánlott cikkek
Ez útmutatóként szolgál a Z és a T pontszám közötti legnagyobb különbséghez. Itt is megvitatjuk a Z pontszám és a T pontszám kulcsfontosságú különbségeit az infographics és az összehasonlító táblázat segítségével. Lehet, hogy megnézi a következő cikkeket is, ha többet szeretne megtudni-
- Pénzügy vs közgazdaságtan - legnagyobb különbség
- Hiány vs adósság - melyik a jobb
- Eszközvásárlás vs részvényvásárlás
- Pénzpiac vs tőkepiac
- Az Altman Z pontszám áttekintése