
A hibaszázalék képlete (Tartalomjegyzék)
- A hibaszázalék képlete
- Példák a hibaképlet határértékére (Excel sablonnal)
- Hibahatár a képlet kalkulátor
A hibaszázalék képlete
A statisztikában kiszámoljuk a konfidencia intervallumot, hogy megtudjuk, hol esik a minta statisztikai adatainak értéke. A konfidenciaintervallumban a minta statisztikája alatt és felett található értéktartományt hibamargónak nevezzük. Más szavakkal, ez alapvetően a minta statisztikájában szereplő hiba mértéke. Minél nagyobb a hibahatár, annál kisebb az eredmények bizalma, mert ezekben az eredményekben az eltérés mértéke nagyon magas. Amint a neve is sugallja, a hibahatár a tényleges eredmények feletti és alatti értéktartomány. Például, ha egy olyan felmérés során kapunk választ, amelyben az emberek 70% -a válaszolt „jónak”, és a hibaarány 5%, ez azt jelenti, hogy általában a lakosság 65–75% -a gondolja úgy, hogy a válasz „jó” .
A hibahatár képlete -
Margin of Error = Z * S / √n
Hol:
- Z - Z pontszám
- S - populáció szórása
- n - Minta mérete
Egy másik képlet a hibahatár kiszámításához:
Margin of Error = Z * √((p * (1 – p)) / n)
Hol:
- p - A minta aránya (a minta sikeres része)
Most, hogy megtalálja a kívánt z-értéket, meg kell ismernie a minta konfidencia-intervallumát, mivel a Z-pont attól függ. Az alábbi táblázat a konfidencia intervallum és a z pontszám kapcsolatát mutatja:
| Megbízhatósági intervallum | Z - Pontszám |
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1, 96 |
| 99% | 2, 58 |
Miután megismerte a konfidencia intervallumot, felhasználhatja a megfelelő z értéket, és onnan kiszámolhatja a hibahatárt.
Példák a hibaképlet határértékére (Excel sablonnal)
Vegyünk egy példát a hibahatár kiszámításának jobb megértéséhez.
A Hibamargó sablon letölthető itt - A Hibamargó sablonA hibás képlet határértéke - 1. példa
Tegyük fel, hogy felmérést végezünk annak megállapítása érdekében, hogy az egyetemi hallgatók milyen pontszámot kapnak. Véletlenszerűen választottunk ki 500 hallgatót, és megkérdeztük az osztályzatot. Ennek átlaga 4-ből 2, 4, a szórás 30%. Tegyük fel, hogy a konfidencia intervallum 99%. Számítsa ki a hibahatárot.
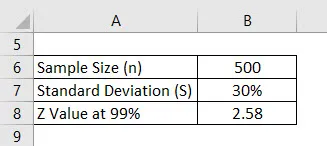
Megoldás:
A hibahatár az alábbiakban megadott képlet alapján kerül kiszámításra
Hibahatár = Z * S / √n
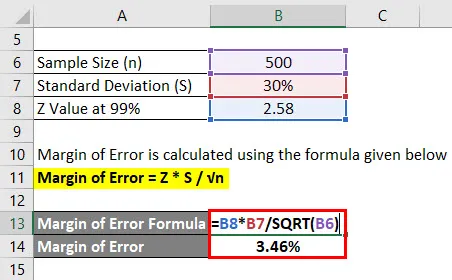
- Hibahatár = 2, 58 * 30% / √ (500)
- Hibahatár = 3, 46%
Ez azt jelenti, hogy 99% -os bizalommal a hallgatók átlagos osztálya 2, 4, plusz vagy mínusz 3, 46%.
A hibás képlet határértéke - 2. példa
Tegyük fel, hogy új egészségügyi terméket dob be a piacon, de félreértheti, hogy melyik íze lesz az embereknek tetszeni. Összezavarodott a banán- és a vaníliaaroma között, és úgy döntött, hogy felmérést készít. Az Ön népessége 500 000, amely a célpiac, és ebből úgy döntött, hogy megkérdezi 1000 ember véleményét, és ez lesz a minta. Tegyük fel, hogy a konfidencia intervallum 90%. Számítsa ki a hibahatárot.
Megoldás:
A felmérés elvégzése után megtudta, hogy 470 embernek tetszett a banán aromája, 530 pedig vanília aromát kért.
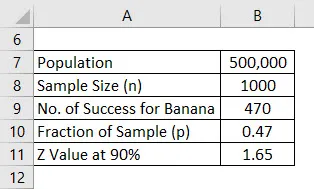
A hibahatár az alább megadott képlet alapján kerül kiszámításra
Hibahatár = Z * √ ((p * (1 - p)) / n)
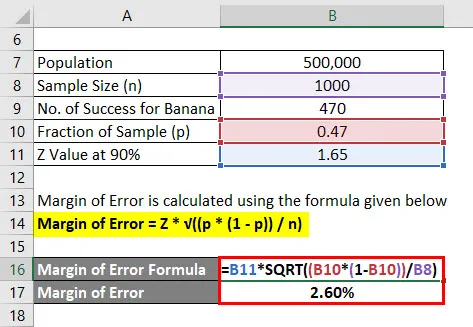
- Hibahatár = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Hibahatár = 2, 60%
Tehát 90% -os bizalommal mondhatjuk, hogy az emberek 47% -ának tetszett a banán íz plusz vagy mínusz 2, 60%.
Magyarázat
Mint fentebb tárgyaltuk, a hibahatár segít megérteni, hogy a felmérés mintázata megfelelő-e vagy sem. Ha a margó hiba túl nagy, akkor előfordulhat, hogy a mintánk túl kicsi, és ezt növelnünk kell, hogy a minta eredményei jobban megfeleljenek a populáció eredményeinek.
Vannak olyan forgatókönyvek, amikor a hibahatár nem lesz sok hasznos, és nem segít nekünk a hiba követésében:
- Ha a felmérés kérdéseit nem úgy tervezték meg, hogy segítenek a szükséges válasz megszerzésében
- Ha a felmérésre válaszolók némi elfogultsággal rendelkeznek annak a terméknek a vonatkozásában, amelyre a felmérést készítik, akkor az eredmény sem lesz túl pontos
- Ha a kiválasztott minta maga a populáció megfelelő képviselője, akkor is az eredmények messze vannak.
Ugyancsak itt egy nagy feltételezés, hogy a lakosság általában megoszlik. Tehát ha a minta mérete túl kicsi, és a populáció eloszlása nem normális, akkor a z pontszámot nem lehet kiszámítani, és a hibát nem tudjuk megtalálni.
A hibamérleg relevanciája és felhasználása
Amikor a mintaadatokat valamilyen releváns választ találunk a populációkészletre vonatkozóan, van bizonyos bizonytalanság és esély arra, hogy az eredmény eltérhet a tényleges eredménytől. A hibahatár megmondja nekünk, hogy mi az eltérés szintje, ott van a minta kimenete. Minimalizálnunk kell a hibaarányt, hogy mintavételi eredményeink a népességre vonatkozó adatok valós történetét ábrázolják. Tehát alacsonyabb a hibahatár, annál jobb lesz az eredmény. A hibahatár kiegészíti és kiegészíti a rendelkezésére álló statisztikai információkat. Például, ha egy felmérés azt találja, hogy az emberek 48% -a inkább inkább otthon tölti a hétvégét, akkor nem lehetünk annyira pontosak, és vannak hiányzó elemek ezen információkban. Amikor itt bevezettünk egy hibahatárot, mondjuk 5% -ot, akkor az eredményt úgy fogják értelmezni, hogy 43–53% -uknak tetszett az ötlet, hogy hétvégén otthon legyen, és ennek teljesen értelme van.
Hibahatár a képlet kalkulátor
Használhatja a következő hibamargó számológépet
| Z | |
| S | |
| √n | |
| Hibahatár | |
| Hibahatár | = |
|
|
Ajánlott cikkek
Ez egy útmutató a Hibamargó képlethez. Itt tárgyaljuk, hogyan lehet kiszámítani a hibahatárot, a gyakorlati példákkal együtt. Kínálunk egy Margin of Error számológépet is letölthető Excel sablonnal. A következő cikkeket is megnézheti további információkért -
- Útmutató az egyenes vonal értékcsökkenési képletéhez
- Példák a párhuzamos idő képletére
- Hogyan lehet kiszámítani az amortizációt?
- A középhatású tétel képlete
- Altman Z pontszám | Meghatározás | Példák
- Értékcsökkenési képlet Példák az Excel sablonnal