
A tényleges kamatláb képlete (Tartalomjegyzék)
- Képlet
- Példák
- Számológép
Mi az a tényleges kamatláb-képlet?
Az „effektív kamatláb” kifejezés a befektetés tényleges éves hozamára utal, amelyet az adott időtartamon belüli kamatbevonás eredményeként nyernek. Ezzel szemben az effektív kamatláb a hitelfelvevő szempontjából tekinthető a hitelfelvétel valódi költségének. Ezt a tényleges éves hozamot vagy az azzal egyenértékű éves kamatlábat is nevezik. Az effektív kamatláb képlete a megállapított kamatláb és az éves összetételű időszakok száma alapján származtatható. Matematikailag ez a következő,
Effective Interest Rate = (1 + i/n) n – 1
hol,
- i = A megadott kamatláb
- n = Összeállítási periódusok száma évente
Példák a tényleges kamatláb-képletre (Excel sablonnal)
Vegyünk egy példát a tényleges kamatláb kiszámításának jobb megértésére.
Itt letöltheti ezt a tényleges kamatláb-képletet Excel sablon - A tényleges kamatláb-képlet Excel sablonHatékony kamatláb-képlet - 1. példa
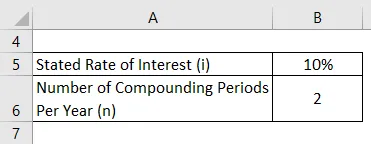
Vegyük például a bejelentett 10% -os kamatlábú befektetést. Számítsa ki az effektív kamatlábat, ha a befektetést évente kétszer kell összeadni.
Megoldás:
A tényleges kamatlábat az alábbiakban megadott képlet alapján számítják ki
Hatékony kamatláb = (1 + i / n) n - 1

- Hatékony kamatláb = (1 + 10% / 2) 2 - 1
- Hatékony kamatláb = 10, 25%
Ezért a jegyzett befektetés tényleges kamatlába 10, 25%.
Hatékony kamatláb-képlet - 2. példa
Vegyük példát Johnra, aki egy olyan kötvény befektetése iránt érdeklődik, amely 9% -os kamatlábat kínál. A keverés jellege azonban eltérő, és John nem biztos abban, hogy melyik keverék fogja a legnagyobb hozamot elérni. Számítsa ki az effektív kamatlábat és segítsen Johnnak, hogy eredményes döntést hozzon a következő összetételi időszakra:
- Évi
- Félévente
- Negyedévenként
- Havi
- Napi
Évi
A tényleges kamatlábat az alábbiakban megadott képlet alapján számítják ki
Hatékony kamatláb = (1 + i / n) n - 1
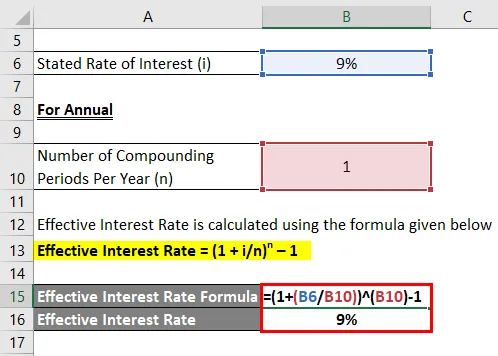
- Hatékony kamatláb = (1 + 9% / 1) 1 - 1
- Hatékony kamatláb = 9%
Félévente
A tényleges kamatlábat az alábbiakban megadott képlet alapján számítják ki
Hatékony kamatláb = (1 + i / n) n - 1
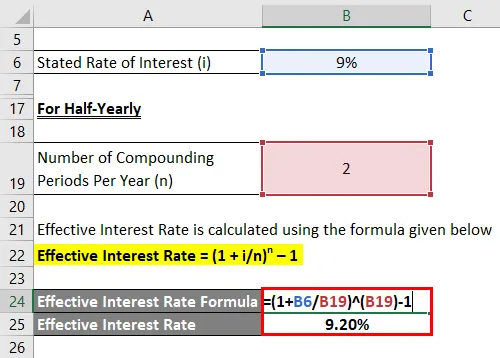
- Hatékony kamatláb = (1 + 9% / 2) 2 - 1
- Hatékony kamatláb = 9, 20%
Negyedévenként
A tényleges kamatlábat az alábbiakban megadott képlet alapján számítják ki
Hatékony kamatláb = (1 + i / n) n - 1
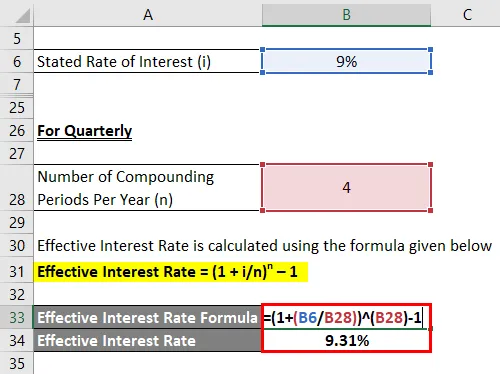
- Hatékony kamatláb = (1 + 9% / 4) 4 - 1
- Hatékony kamatláb = 9, 31%
Havi
A tényleges kamatlábat az alábbiakban megadott képlet alapján számítják ki
Hatékony kamatláb = (1 + i / n) n - 1
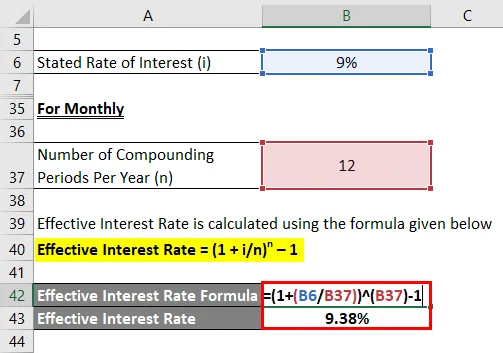
- Hatékony kamatláb = (1 + 9% / 12) 12 - 1
- Hatékony kamatláb = 9, 38%
Napi
A tényleges kamatlábat az alábbiakban megadott képlet alapján számítják ki
Hatékony kamatláb = (1 + i / n) n - 1

- Hatékony kamatláb = (1 + 9% / 365) 365 - 1
- Hatékony kamatláb = 9, 42%
Ezért egyértelműen látható, hogy az éves hozam növekszik az évente bekövetkező kompozíciók számának növekedésével. Mint ilyen, a napi keverés a legjobb hozamot nyújtja Johnnak (tényleges kamat 9, 38%, szemben a megadott 9% kamatlábbal).
Magyarázat
Az effektív kamatláb képlete az alábbi lépésekből származtatható:
1. lépés: Először határozza meg a beruházás megadott kamatlábát, amelyet általában a beruházási dokumentum említ. Ezt 'i' jelöli.
2. lépés: Ezután számolja ki az összeállítási periódusok számát egy év alatt, és azt „n” -vel jelöli. Az összekeverést általában negyedévente, félévente és évente hajtják végre, ami azt jelenti, hogy évente 4, 2 és 1 összekeverés történik.
3. lépés: Végül az effektív kamatláb képlete származtatható a megadott kamatláb (1. lépés) és évente számított összeállítási periódusok (2. lépés) felhasználásával, az alábbiak szerint.
Hatékony kamatláb = (1 + i / n) n - 1
A hatékony kamatláb-formula relevanciája és felhasználása
Fontos megérteni az effektív kamatláb fogalmát, mivel ez alapvető mutató egy befektető vagy egy másik pénzügyi felhasználó számára. A befektetők elsősorban az effektív kamatlábat használják, mivel ez a befektetésből származó tényleges hozam. Mint ilyen, a befektetők nagyobb hangsúlyt fektetnek az összetett évek számára, mivel a nagyobb összegek nagyobb hozamot eredményeznek. Másrészt a perspektíva megváltozik egy olyan hitelfelvevő esetében, aki évente kevesebb összeget keres, mivel ez alacsonyan tartaná kamatköltségüket és jobb jövedelmezőséget eredményezne.
Az effektív kamatláb fogalma nagyon függ attól, hogy egy év alatt megtörténik-e olyan kamatkezelés, amely végül magasabb hozammal, vagy végül magasabb visszaváltási értékkel a lejáratkor. Általában az effektív éves ráta növekszik az összetett évek számának növekedésével. Bár az összekeverés végtelen számú alkalommal megtehető, szem előtt kell tartani, hogy a keverési hatásnak van egy bizonyos korlátja, amelyen túl a jelenség megszűnik. Ezt a típusú vegyületet folyamatos keverésnek nevezzük, amelynek effektív kamatlábát kifejezzük - e i, i a megadott kamatláb, és független az összeállítási periódustól.
Hatékony kamatláb-kalkulátor
Használhatja a következő tényleges kamatláb-számológépet
| én | |
| n | |
| Hatékony kamatláb | |
| Hatékony kamatláb = | (1 + i / n) n -1 |
| = | (1 + 0/0) 0 -1 = 0 |
Ajánlott cikkek
Ez egy útmutató a tényleges kamatláb-képlethez. Itt tárgyaljuk, hogyan lehet kiszámítani a tényleges kamatlábat, a gyakorlati példákkal együtt. Mi is rendelkezésre áll egy hatékony kamatláb-kalkulátor letölthető Excel sablonnal. A következő cikkeket is megnézheti további információkért -
- A havi összetett kamat képlete
- Hogyan lehet kiszámítani a nominális kamatlábat?
- Példák a kamatkiadásra
- A nominális GDP-képlet kiszámítása
- Kamat vs osztalék A 8 legfontosabb különbség, amelyet tudnia kell