
Bevezetés a hash funkcióba C
Ez a cikk röviden ismerteti a hashizálást (hash table és hash function). A legfontosabb fogalom a „keresés”, amely meghatározza az idő bonyolultságát. Az idő bonyolultságának csökkentése érdekében bevezettük az összes többi adatszerkezet kivágási koncepcióját, amelynek átlagos esetben O (1) ideje van, és a legrosszabb esetben O (n) idő szükséges.
A hashizálás olyan technika, amely gyorsabb hozzáférést biztosít az elemekhez, és amely az adott adatokat egy kevesebb kulccsal leképezi az összehasonlításhoz. Általában ebben a technikában a kulcsok kivonat-függvény segítségével kerülnek nyomon követésre a hash táblának ismert táblává.
Mi a hasmenés funkció?
A hash-függvény egy olyan funkció, amely állandó időtartamú műveletet használ az érték tárolására és lekérésére a hash-táblából, amelyet a kulcsokon egész számként alkalmaznak, és amelyet a hash-táblázat értékeinek címeként használnak.
A hasítási funkció típusai
A hash-funkciók típusait az alábbiakban ismertetjük:
1. Osztási módszer
Ennél a módszernél a hash-függvény az osztódás fennmaradó részétől függ.
Példa: a hash táblába helyezendő elemek 42, 78, 89, 64 lehetnek, és a táblázat méretét 10-nek vesszük.
Hasadás (kulcs) = elemek% táblaméret;
2 = 42% 10;
8 = 78% 10;
9 = 89% 10;
4 = 64% 10;
A táblázat ábrázolása az alábbiak szerint látható:
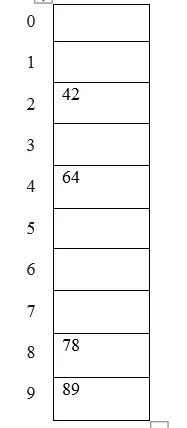
2. Középső tér módszer
Ebben a módszerben a négyzet alakú elem középső részét vesszük indexként.
A hash táblába elhelyezett elem 210, 350, 99, 890 és az asztal mérete 100.
210 * 210 = 44100, index = 1, mivel az eredmény (44100) középső része 1.
350 * 350 = 122500, index = 25, mivel az eredmény (122500) középső része 25.
99 * 99 = 9801, index = 80, mivel az eredmény (9801) középső része 80.
890 * 890 = 792100, index = 21, mivel az eredmény (792100) középső része 21.
3. Digit összehajtogatási módszer
Ebben a módszerben az a táblázatba elhelyezésre kerülő elem énekes hash-kulcs, amelyet úgy kapnak, hogy az elemeket különféle részekre osztják, majd egyesítik az alkatrészeket néhány egyszerű matematikai művelet végrehajtásával.
Helyezendő elem a 23576623, 34687734.
- hash (kulcs) = 235 + 766 + 23 = 1024
- hash-kulcs) = 34 + 68 + 77 + 34 = 213
Tegyük fel, hogy ezeknek a hashizálási típusoknak száma 1- 100 és a hash tábla mérete = 10. Elemek = 23, 12, 32
Hasadás (kulcs) = 23% 10 = 3;
Hasadás (kulcs) = 12% 10 = 2;
Hasadás (kulcs) = 32% 10 = 2;
A fenti példa alapján észre kell venni, hogy mind a 12., mind a 32. elem a 2. helyre utal a táblázatban, ahol nem lehet írni mindkettőt ugyanazon a helyen, ezt a problémát ütközésnek nevezzük. Az ilyen jellegű problémák elkerülése érdekében alkalmazhatók kivonat-funkciók néhány technikája.
Az ütközésmegoldási technikák típusai
Beszéljünk meg az ütközések megoldásának technikáira:
1. Láncolás
Ebben a módszerben, amint a neve is sugallja, ez egy dobozláncot biztosít a táblázatban szereplő rekordhoz, amely két elemmel rendelkezik. Tehát ha ilyen ütközések történnek, akkor a négyzetek összekapcsolt lista formájában működnek.
Példa: 23., 12., 32. táblázat 10 méretű táblával.
Hasadás (kulcs) = 23% 10 = 3;
Hasadás (kulcs) = 12% 10 = 2;
Hasadás (kulcs) = 32% 10 = 2;
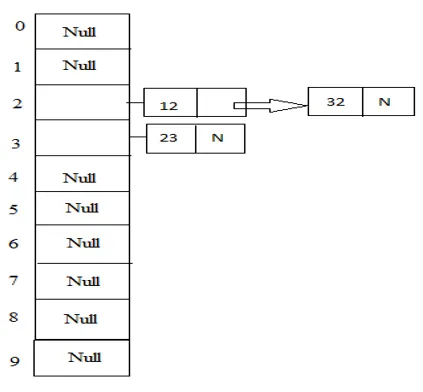
2. Nyissa meg a Címzés lehetőséget
- Lineáris szondázás
Ez egy másik módszer az ütközési problémák megoldására. Mivel a név azt mondja, amikor ütközés történik, akkor két elemet kell elhelyezni a táblázat ugyanazon bejegyzésén, de ezzel a módszerrel megkereshetjük a következő üres helyet vagy bejegyzést a táblázatban, és elhelyezhetjük a második elemet. Ez ismét egy másik problémához vezethet; ha a táblázatban nem található üres bejegyzés, akkor ez fürtözéshez vezet. Ezért klaszterproblémaként ismert, amelyet a következő módszerrel lehet megoldani.
Példa: 23., 12., 32. táblázat 10 méretű táblával
Hasadás (kulcs) = 23% 10 = 3;
Hasadás (kulcs) = 12% 10 = 2;
Hasadás (kulcs) = 32% 10 = 2;

Ebben a diagramban a 12 és a 32 elhelyezhetők ugyanabban a bejegyzésben a 2. mutatóval, de ezzel a módszerrel lineárisan helyezkednek el.
- Másodlagos próba
Ez a módszer a klaszterprobléma megoldására szolgál a lineáris tapintás során. Ebben a módszerben a hash-funkcióval rendelkező hash-függvényt a következőképpen kell kiszámítani: hash (kulcs) = (hash (kulcs) + x * x) a táblázat% -a (ahol x = 0, 1, 2…).
Példa: 23., 12., 32. táblázat 10 méretű táblával
Hasadás (kulcs) = 23% 10 = 3;
Hasadás (kulcs) = 12% 10 = 2;
Hasadás (kulcs) = 32% 10 = 2;

Ebben láthatjuk, hogy a 23-as és a 12-es könnyen elhelyezhetők, de a 32-es nem ugyanazok, mint a 12-es és a 32-es ugyanaz a bejegyzés ugyanazzal a mutatóval a táblázatban, mivel ezen módszer szerint hash (kulcs) = (32 + 1 * 1) % 10 = 3. De ebben az esetben a 3. indexű tábla bejegyzését 23-ra tesszük, tehát x értéket kell 1-rel növelnünk. Hash (kulcs) = (32 + 2 * 2)% 10 = 6, tehát most el tudjuk helyezni 32 a bejegyzésben, a táblázat 6. mutatójával.
- Dupla kivonatolás
Ehhez a módszerhez 2 hash függvényt kell kiszámítanunk az ütközési probléma megoldásához. Az elsőt egyszerű osztásos módszerrel számolják. A másodiknak meg kell felelnie két szabálynak; nem lehet 0-val egyenlő, és a bejegyzéseket próbára kell venni.
- 1 (kulcs) = kulcs% -a tábla méretét.
- 2 (kulcs) = p - (kulcs mod p), ahol p prímszámok <a táblázat mérete.
Példa: 23., 12., 32. táblázat 10 méretű táblával
Hasadás (kulcs) = 23% 10 = 3;
Hasadás (kulcs) = 12% 10 = 2;
Hasadás (kulcs) = 32% 10 = 2;
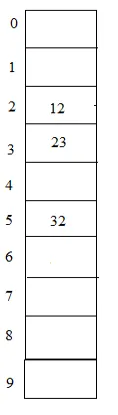
Ebben ismét a 32 elemet el lehet helyezni hash2 (kulcs) = 5 - (32% 5) = 3 használatával. Tehát a 32 az üres táblázat táblázatához az 5. mutatóra helyezhető, mivel 3 bejegyzésnek ki kell ugrania az elhelyezéshez.
Összegzés-hasító függvény C-ben
A hashizálás az egyik legfontosabb módszer az adatok keresése szempontjából, nagyon hatékony és gyors módszerekkel, kivonat-függvény és hash-táblák felhasználásával. Minden elem kereshető és elhelyezhető különféle kivonási módszerekkel. Ez a technika az idő együtthatója szempontjából nagyon gyors, mint bármely más adatszerkezet.
Ajánlott cikkek
Ez egy útmutató a hash-funkcióhoz C.-ban. Itt tárgyaljuk a hashing-funkció bevezetését a C-ben, Mi a hash-függvény, a hash-funkció típusai stb.
- Kivonás a DBMS-ben
- Titkosítási folyamat
- Hogyan lehet telepíteni a CakePHP-t?
- Hogyan működik a blokklánc?
- Hashing funkció Java-ban
- Kivonási funkció a PHP-ben Hogyan dolgozz?