
Bevezetés a DFS algoritmusba
A DFS az első mélységű keresési algoritmus, amely a grafikon minden egyes csomópontjának áthaladását biztosítja a csomópontok megismétlése nélkül. Ez az algoritmus megegyezik a fa mélységének első átjárásával, de különbözik a logikai érték fenntartásában annak ellenőrzése érdekében, hogy a csomópontot már meglátogatták-e vagy sem. Ez fontos a gráf áthaladása szempontjából, mivel a ciklusok is vannak a gráfban. Ebben az algoritmusban verem van fenntartva a felfüggesztett csomópontok tárolása közben. Azért nevezték el, mert először az egyes szomszédos csomópontok mélységére haladunk, majd tovább haladunk egy másik szomszédos csomóponton.
Magyarázza el a DFS algoritmust
Ez az algoritmus ellentétes a BFS algoritmussal, ahol az összes szomszédos csomópontot meglátogatják a szomszédos szomszédok a szomszédos csomópontokhoz. Megkezdi a grafikon feltárását az egyik csomópontról, és feltárja annak mélységét, mielőtt visszahúzódna. Két dolgot vesz figyelembe ebben az algoritmusban:
- Látogatás a Vertexnél: A grafikon csúcsának vagy csomópontjának kiválasztása az áthaladáshoz.
- Vertex feltárása: A csúcshoz szomszédos összes csomópont áthaladása.
Pszeudo kód a mélység első kereséséhez :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
A DFS-hez a Lineáris Átmenetek is léteznek, amelyek háromféle módon valósíthatók meg:
- Előrendelés
- inorder
- postorder
A fordított postai postázás nagyon hasznos módja a topológiai rendezésben, valamint a különféle elemzéseknek. A csomópontot szintén fenntartják azoknak a csomópontoknak a tárolására, amelyek feltárása még folyamatban van.
Grafikon áthaladás DFS-ben
A DFS-ben az alábbi lépéseket kell követnünk a grafikon áthaladásához. Például egy adott gráf, kezdjük az átjárást az 1-től:
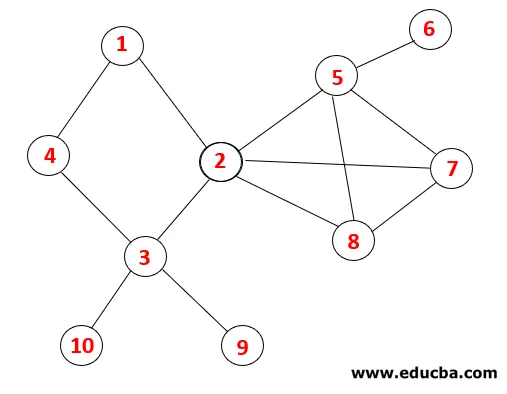
| Kazal | Átmeneti sorrend | Feszítőfának |
| 1 |  |
|
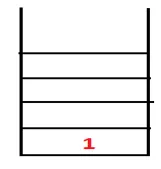 | 1, 4 |  |
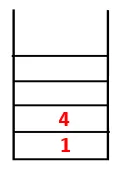 | 1, 4, 3 |  |
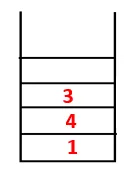 | 1, 4, 3, 10 | 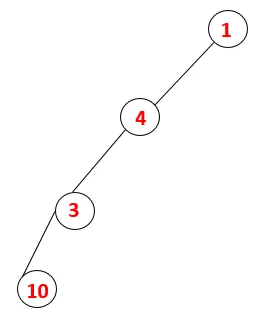 |
 | 1, 4, 3, 10, 9 | 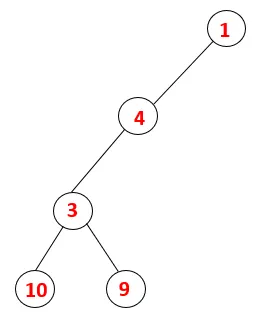 |
 | 1, 4, 3, 10, 9, 2 | 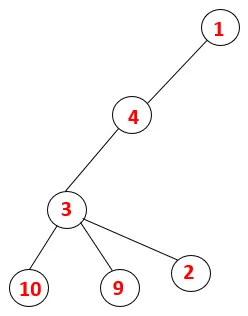 |
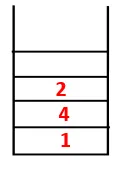 | 1, 4, 3, 10, 9, 2, 8 |  |
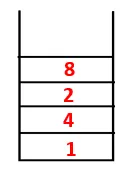 | 1, 4, 3, 10, 9, 2, 8, 7 | 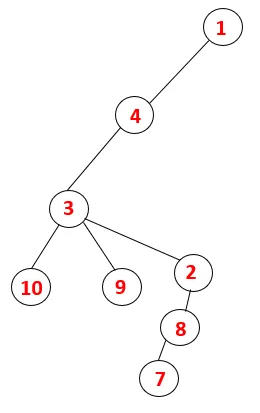 |
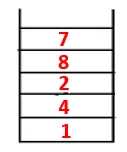 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
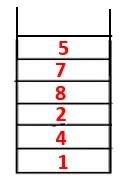 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 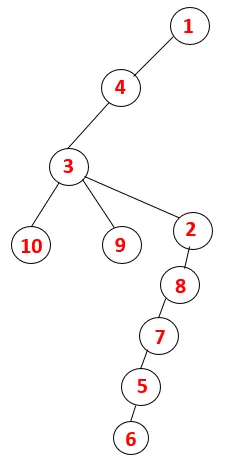 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 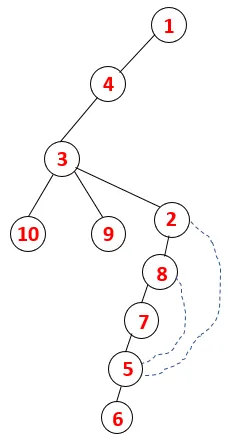 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
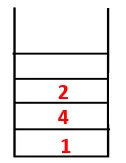 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 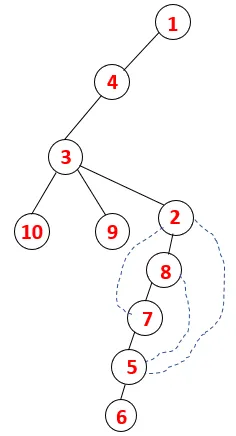 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 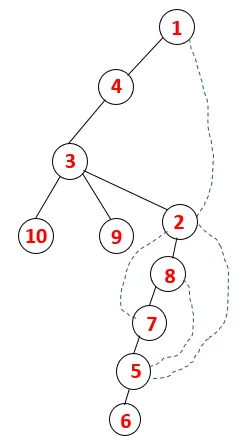 |
Magyarázat a DFS algoritmushoz
Az alábbiakban olvashatjuk el a DFS algoritmus előnyeit és hátrányait:
1. lépés: Az 1. csomópont meglátogatásra kerül, és hozzáadódik a szekvenciához, valamint az átfogó fához.
2. lépés: Felfedezzük az 1 szomszédos csomópontjait, vagyis 4, tehát 1-t veremre toljuk, és 4-et beillesztjük a sorozatba, valamint az átfogó fába.
3. lépés: A szomszédos 4 csomópontok egyikét felfedezzük, így 4-et a verembe toljuk, és 3 belép a szekvencia és az átfogó fába.
4. lépés: A 3 szomszédos csomópontokat felfedezzük úgy, hogy ráhelyezzük a veremre, és 10 belép a sorozatba. Mivel a 10-ig nincs szomszédos csomópont, így a 3 kiugrik a veremből.
5. lépés: Egy másik szomszédos 3 csomópontot vizsgálnak meg, 3-at ráhelyeznek a veremre, és meglátogatják a 9-et. Nincs 9 szomszédos csomópont, így a 3 kiugrik, és meglátogatja az utolsó szomszédos csomópontot, azaz a 3-at.
Hasonló folyamatot követünk minden csomóponton, amíg a verem ki nem ürül, ami jelzi a haladási algoritmus leállási állapotát. - -> A szaggatott fán a szaggatott vonal a grafikon hátsó széleire utal.
Ily módon a gráfban minden csomópont áthalad, anélkül hogy megismételné egyik csomópontot sem.
Előnyök és hátrányok
- Előnyök: Ennek az algoritmusnak a memóriaigénye nagyon alacsony. Kevesebb hely- és időbonyolultság, mint a BFS-nél.
- Hátrányok: A megoldás nem garantált. Topológiai rendezés. Grafikon hidainak megtalálása.
Példa a DFS algoritmus megvalósítására
Az alábbiakban bemutatjuk a DFS algoritmus megvalósításának példáját:
Kód:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Kimenet:
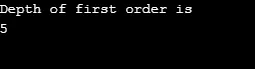
Magyarázat a fenti programra: Készítettünk egy 5 csúcsot (0, 1, 2, 3, 4) tartalmazó gráfot, és a meglátogatott tömböt használtuk az összes meglátogatott csúcs nyomon követésére. Ezután minden olyan csomópontnál, amelynek szomszédos csomópontjai léteznek, ugyanaz az algoritmus ismétlődik, amíg az összes csomópontot meg nem látogatják. Ezután az algoritmus visszatér a csúcs hívására, és felugrik a veremből.
Következtetés
Ennek a grafikonnak a memóriaigénye kevesebb a BFS-hez képest, mivel csak egy verem kell fenntartani. Ennek eredményeként létrejön egy DFS-t átfogó fa és átjárási sorrend, de nem állandó. A választott kiindulási és felfedezési csúcsoktól függően több áttörés is lehetséges.
Ajánlott cikkek
Ez egy útmutató a DFS algoritmushoz. Itt lépésről lépésre magyarázzuk meg, ábrázoljuk az ábra előnyeit és hátrányait táblázat formátumban. Megnézheti más kapcsolódó cikkeket is, ha többet szeretne megtudni -
- Mi az a HDFS?
- Mély tanulási algoritmusok
- HDFS parancsok
- SHA algoritmus