
Binomial Distribution Formula (Tartalomjegyzék)
- Képlet
- Számológép
- Példák Excel sablonnal
Mi a binomiális eloszlási képlet?
A binomiális eloszlás az a valószínűség-eloszlási képlet, amely összegzi annak valószínűségét, hogy egy esemény megadott paraméterek vagy feltételezések esetén A nyer, B veszít vagy fordítva. Van azonban a binomiális eloszlás mögöttes feltételezése, ahol minden vizsgálathoz csak egy eredmény lehetséges, akár siker, akár veszteség. És minden egyes vizsgálat önmagában kizárja egymástól.
Tegyük fel, hogy ha a kettő közül egyet értünk, akkor azt sikerként definiáljuk, akkor az N kísérletből kiszámított x siker valószínűségét az alábbiak szerint lehet kiszámítani:
P(X) = n C x * p x * (1 – p) (nx)
P(X) = (n! / (x! * (n – x)!)) * p x * (1 – p) (nx)
Ahol p az egy próba sikerességének valószínűsége.
Példák a binomiális eloszlási képletre
Vegyünk egy példát a binomiális eloszlás kiszámításának jobb megértéséhez.
Itt töltheti le a Binomial Distribution Formula Excel sablont - Binomial Distribution Formula Excel TemplateBinomiális eloszlásképlet - 1. példa
Egy érmét tízszer megfordítanak. Számítsa ki az 5 fej megszerzésének valószínűségét egy Binomial eloszlásképlet segítségével.

Megoldás:
A valószínűséget az alábbiakban megadott binomiális eloszlási képlettel számítják ki
P (X) = (n! / (X! * (N - x)!)) * P x * (1 - p) (nx)

- P (x = 5) = (10! / (5! * (10 - 5)!)) * (0, 5) 5 * (1 - 0, 5) (10 - 5)
- P (x = 5) = (10! / (5! * 5!)) * (0, 5) 5 * (0, 5) 5
- P (x = 5) = 0, 2441
Pontosan 5 siker elérésének valószínűsége 0.2461
Binomiális eloszlásképlet - 2. példa
Egy tanulmány szerint kiderült, hogy a kedvtelésből tartott állatok biztosítását vásárló emberek 70% -a főként nő. Ha véletlenszerűen választanánk ki 9 háziállatbiztosítási tulajdonosot. Mi a valószínűsége, közülük 7 nő lesz?

Megoldás:
A valószínűséget az alábbiakban megadott binomiális eloszlási képlettel számítják ki
P (X) = (n! / (X! * (N - x)!)) * P x * (1 - p) (nx)
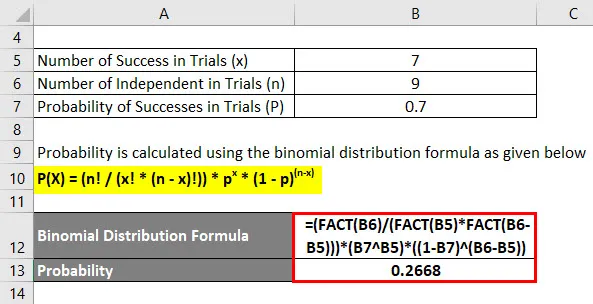
- P (x = 7) = (9! / (7! * (9 - 7)!)) * (0, 7) 7 * (1 - 0, 7) (9 - 7)
- P (x = 7) = (9! / (7! * 2!)) * (0, 7) 7 * (0, 3) 2
- P (x = 7) = 0, 2668
Binomiális eloszlásképlet - 3. példa
Tavaly az Autocar India felmérésében kiderült, hogy a sportautók vásárlóinak 70% -a férfi. Ha 10 sportautó-tulajdonos véletlenszerűen kerül kiválasztásra. Mi a valószínűsége, közülük 6 ember lesz?

Megoldás:
A valószínűséget az alábbiakban megadott binomiális eloszlási képlettel számítják ki
P (X) = (n! / (X! * (N - x)!)) * P x * (1 - p) (nx)

- P (x = 5) = (10! / (6! * (10 - 6)!)) * (0, 7) 6 * (1 - 0, 7) (10 - 6)
- P (x = 5) = (10! / (6! * 4!)) * (0, 7) 6 * (0, 3) 4
- P (x = 5) = 0, 2001
Magyarázat
A binomiális eloszlás alapvetően sokkal inkább függ a kísérletek vagy megfigyelések számától. Míg mindegyik próba meghatározza a kimenetele értékének valószínűségét, vagy más szavakkal. A binomiális véletlen változó az x sikeres kimenetele a binomiális kísérlet ismételt kipróbálásának n számában. Míg a binomiális véletlen változó valószínűség-eloszlását binomiális eloszlásnak is nevezzük.
Ha például egy érmét dobunk, akkor a fej megszerzésének valószínűsége a 100% -ból 50, 50% -ot tesz ki. Ha 100 kísérletet hajtunk végre. A kinyerőfejek várható értéke 50 (100 x 0, 5). A binomiális eloszlás egy statisztikai kifejezés, amely megjósolja egy esemény kimenetelét, például annak a valószínűségét, hogy egy sportoló megnyeri a versenyt.
Vannak bizonyos lépések és szabályok a Binomial Distribution modellek speciális kritériumainak teljesítéséhez a képlet felhasználása érdekében.
1. lépés: Javított kísérletek
Ebben a lépésben van egy rögzített számú próba, amely nem változtatható meg a teljes folyamat során. A binomiális valószínűségi képletben a kísérletek számát „n” betű képviseli. Esetünkben érme lefordítása, szabad dobások, kerékpörgetések a rögzített próbaidők.
2. lépés: Független kísérletek
A független vizsgálat a binomiális valószínűség további feltétele, amelyben a vizsgálatok függetlenek egymástól, ha az egyik vizsgálat eredménye nem befolyásolja sokkal jobban a következő kísérleteket.
Ha egy példát veszünk, ahol a független kísérletek során érmét vagy dobókockát dobhatunk el, az független a következő eseményektől.
3. lépés: A siker rögzített valószínűsége
Az ilyen típusú eloszlás esetén a siker valószínűsége minden kísérletnél azonos marad. Például, ha eldobunk egy érmét, akkor minden esemény kimenetelének valószínűsége akár a fej, akár a farok értéke 0, 5. Mivel két lehetséges eredmény lehetséges.
4. lépés: Két kölcsönösen kizáró eredmény
Ebben az eloszlásban csak kétféle, egymást kizáró eredmény létezik: siker vagy kudarc. Ahol a sikert pozitívan határozták meg. A próba célja annak igazolása, amit sikerként definiáltunk. Vagy pozitív, vagy negatív.
A binomiális eloszlási formula relevanciája és felhasználása
A binomiális eloszlási modell a legfontosabb valószínűségi modell, amelyre szükség van, ha két lehetséges eredmény várható. Akkor jön létre, amikor kettőnél több különálló eredmény volt. Ebben az esetben a multinomális valószínűség megfelelőbb. De itt a legnagyobb aggodalom inkább a helyzetet illeti, ahol az eredmény kettős.
A binomiális eloszlás használatához három modellre van szükség:
- A folyamat minden kimenetele eredményt eredményez vagy kudarcot eredményez.
- Az egyes folyamatok eredménye ugyanazt a valószínűséget eredményezi.
- Valamennyi eredmény kölcsönösen kizárja a folyamatot.
Binomial Distribution Formula Calculator
Használhatja a következő Binomial Distribution Calculator-ot
| n | |
| p | |
| x | |
| Binomiális eloszlásképlet | |
| Binomiális eloszlásképlet = | (n! / x! * (n - x)!) * p x * (1 - p) n - x | |
| (0! / 0! * (0 - 0)!) * 0 0 * (1 -0) 0-0 = | 0 |
Binomiális eloszlásképlet Excelben (Excel sablonnal)
Az alábbiakban bemutatunk egy újabb példát az Excelben a binomiális eloszlásról. Nagyon könnyű és egyszerű.
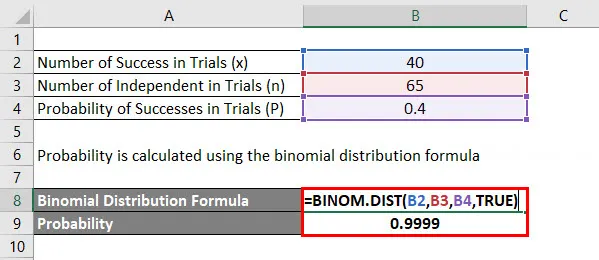
Számítsa ki a binomális eloszlást Excelben a BINOM.DIST függvény használatával.
Az alábbiakban a Binomial Distribution formula szintaxisa található az Excelben.

Ahol a Binomial eloszlás a következő érvet használja:
- Számok: Meghatározza a próba sikereinek számát.
- Kísérletek: független vizsgálatok száma
- Probabiity_s: A siker valószínűsége minden kísérletnél.
- Kumulatív: Lehetővé teszi logikai érték kiválasztását, igaz vagy hamis értékkel.

A valószínűséget a binomiális eloszlási képlet alapján számítják ki
Ajánlott cikkek
Ez egy útmutató a Binomial Distribution Formula-hoz. Itt tárgyaljuk, hogyan lehet kiszámítani a binomiális eloszlást, és a gyakorlati példákat is. Binomial Distribution kalkulátort is letölthetünk az Excel sablonnal. A következő cikkeket is megnézheti további információkért -
- A középhatárérték-tétel képlete
- Normál normál eloszlási képlet
- A normál eloszlás kiszámítása
- A T eloszlási képlet