Hatékony éves kamatláb (tartalomjegyzék)
- Képlet
- Példák
- Számológép
Mi az a tényleges éves kamatképlet?
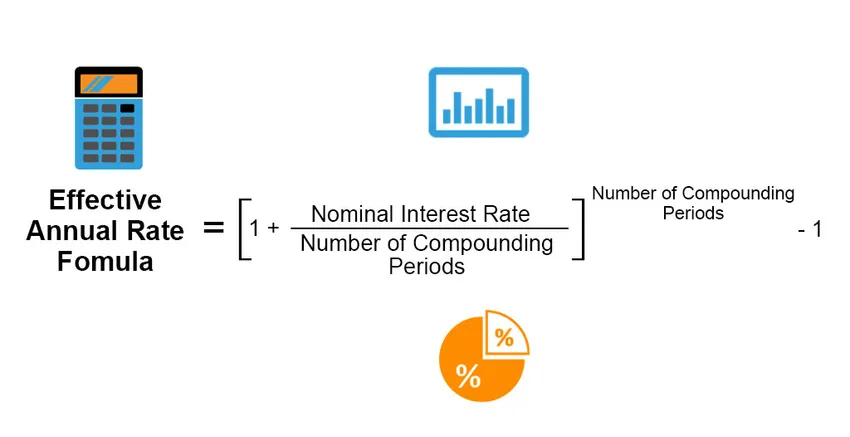
A tényleges éves kamat az a tényleges kamatláb, amelyet befektetéssel, kölcsönrel vagy hasonló pénzügyi termékkel keresnek vagy fizetnek ki, és egyébként különbözik a „nominális kamatlábtól”, mert a kamatfizetési időszak, a kamat összekeverése, az összes a kölcsön vagy a befektetés időtartama stb. A tényleges éves kamatot a következő képlettel kell kiszámítani;
Effective Annual Rate = ((1 + (Nominal Interest Rate / Number of Compounding Periods)) Number of Compounding Periods) – 1
Példák a tényleges éves kamatképletre (Excel sablonnal)
Vegyünk egy példát a tényleges éves kamat kiszámításának jobb megértésére.
Itt töltheti le a Hatékony éves kamatláb-képlet Excel sablont - A Hatékony éves kamatláb-sablon ExcelHatékony éves kamatképlet - 1. példa
Tegyük fel, hogy X úr személyes kölcsönt vesz fel egy bankból 20% -os kamatlábbal, évente félévenként. Az információk felhasználásával kiszámítsa a tényleges éves rátát.

Megoldás:
A tényleges éves rátát az alábbiakban megadott képlettel számolják
Hatékony éves kamat = ((1 + (névleges kamatláb / összeállítási periódusok száma)) összevont periódusok száma) - 1

- Hatékony éves ráta = ((1 + (20% / 2)) 2) - 1
- Hatékony éves ráta = 21%
Hatékony éves kamatképlet - 2. példa
Tegyük fel, hogy A úr 100 dollárt fektetett be betéti igazolásba, amely negyedévenként 10% -os nominális kamatot fizet ki. Számítsa ki a tényleges éves rátát.

Megoldás:
A tényleges éves rátát az alábbiakban megadott képlettel számolják
Hatékony éves kamat = ((1 + (névleges kamatláb / összeállítási periódusok száma)) összevont periódusok száma) - 1
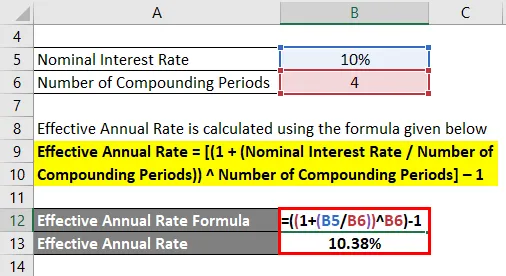
- Hatékony éves ráta = ((1 + (10% / 4)) 4) - 1
- Hatékony éves ráta = 10, 38%
Hatékony éves kamatképlet - 3. példa
Tegyük fel, hogy a befektetési alapok befektetései bevételként 15, 50% -os éves kamatot vonnak le, míg a P2P Hitelezés havi összetett éves nominális kamatlábat 15% -kal keres. Tehát számolja ki a tényleges éves rátát mindkét esetben.

Megoldás:
A tényleges éves rátát az alábbiakban megadott képlettel számolják
Hatékony éves kamat = ((1 + (névleges kamatláb / összeállítási periódusok száma)) összevont periódusok száma) - 1
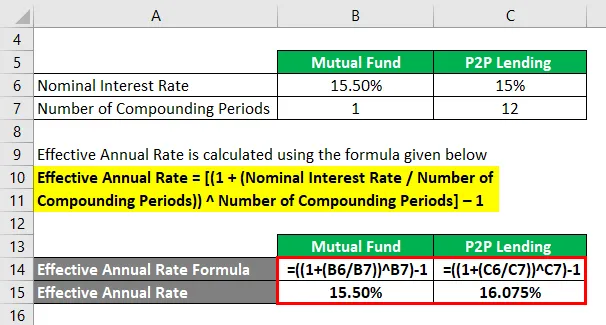
A befektetési alap számára
- Hatékony éves ráta = ((1 + (15, 50% / 1)) 1) - 1
- Hatékony éves ráta = 15, 50%
P2P hitelezéshez
- Hatékony éves ráta = ((1 + (15% / 12)) 12) - 1
- Hatékony éves ráta = 16, 075%
Magyarázat
A nominális kamatláb a pénzügyi termékre megadott kamatláb. A 3. példában a termékekre feltüntetett nominális kamatláb teszi a befektetési alapot a befektetők számára előnyben részesített befektetési módszernek, mert a megszerzett kamat 0, 50% -kal magasabb éves nominális kamatlába miatt.
A tényleges éves kamatlábat azonban úgy számítják ki, hogy figyelembe veszik a nominális éves kamatlábat és összeadják azt a meghatározott időszakok számára (12, ha az összeállítás havi; 6, ha az összeállítás kéthavonta; 4, ha negyedéves, és 2, ha félévente) egyéves időtartamra alkalmazandó. A befektetési alap esetében az összevont idõszakok száma évente 1, míg a P2P hitelezés esetén havi összeállítás, tehát 12 összevont idõszak van.
A képlet alapján
Hatékony éves hozam = ((1 + (nominális kamatláb / összeállítási periódusok száma)) (összevont periódusok száma)) - 1
A befektetési alap tényleges éves hozama = (((1 + (15, 50% / 1)) 1) - 1 = 15, 50%
P2P hitelezés tényleges éves hozama = (((1 + (15, 00% / 12)) 12) - 1 = 16, 075%
A hatékony éves kamatképlet relevanciája és felhasználása
Az effektív éves kamatképletet alkalmazzák a tényleges IRR (belső megtérülési ráta) vagy az évesített hozam megkülönböztetésére egy olyan kamatláb esetében, amely egy adott idõszak során többszörösen összekapcsolódhat vagy nem. Ezt nagyon jól lehet használni a különféle befektetési lehetőségek vagy a különböző struktúrák keretében igénybe vehető hitelkeretek összehasonlításához.
Tegyük fel, hogy két befektetési lehetõség van, a postahivatali betétek és a banki lekötött betétek, amelyekre a befektetõ korlátozta, figyelembe véve kockázati étvágyát és alkalmasságát. A befektető végső célja az, hogy a legtöbbet hozza ki ezekből a betétekből és magasabb hozamot érjen el. Ugyanakkor mindkét instrumentum kissé eltérő kamatlábakat kínál, míg a postahivatali betétek negyedéves kamatot kínálnak a tárgyidőszakra.
- Beruházási összeg: Rs. 10 lakhs
- A befektetés időtartama: 5 év
- Banki betét: 7, 5% éves kamat
- Postahivatal: 7, 4% éves kamat, negyedévenként
A kínált éves kamatlábak alapján úgy tűnik, hogy a jobb választás a banki fix betét. Ha azonban a befektető ténylegesen kiszámítja a posta lekötött betétének negyedéves összevont tényezőjét, akkor annak eredményes éves kamatlába / hozama 7, 61%.
Ennek a tényleges kamatlábnak a 7, 4% -ról 7, 61% -ra történő kis változása miatt a befektető összesen R-t keresne. Ebből a hangszerből 4, 42, 848, 28, míg ő R-t keresett volna. 3 355 469, 14 a banki fix betéti eszközből.
Ha a befektető elmulasztja ezt a tényleges éves kamatot kiszámítani, akkor elvesztette volna a lehetőséget, hogy körülbelül R-nél többet szerezzen. 1 lakh befektetéséből.
Hatékony éves árfolyam-számológép
Használhatja a következő Hatékony éves kamatszámológépet
| Névleges kamatláb | |
| Összeállítási periódusok száma | |
| Hatékony éves ráta | |
| Hatékony éves ráta = | ((1 + (Névleges kamatláb / Összeállítási periódusok száma )) Összegzési periódusok száma ) - 1 | |
| ((1 + (0/0)) 0 ) - 1 = | 0 |
Ajánlott cikkek
Ez egy útmutató a hatékony éves kamatképlethez. Itt tárgyaljuk, hogyan lehet kiszámítani a tényleges éves rátát, valamint a gyakorlati példákat. Kínálunk egy hatékony éves kamatszámológépet is letölthető Excel sablonnal. A következő cikkeket is megnézheti további információkért -
- Számológép a reálkamatláb-képlethez
- A tőkemegtérülési képlet megtérülése Meghatározás
- Hogyan lehet kiszámítani a tényleges kamatlábat?
- Mi a járadékképlet jelenlegi értéke?