Bevezetés az egyesítési szortírozási algoritmusokhoz Java-ban
Az egyesítési rendezési algoritmusok nagyon fontosak a számítástechnikában. A rendezés eredménye a lista elemeinek bizonyos sorrendbe rendezése (növekvő vagy csökkenő). Az egyesítés a rendelkezésre álló egyik leghatékonyabb rendezési algoritmus, mivel az a felosztás és a hódítás fogalmán alapul. Ahogy a neve is sugallja, előbb ossza meg a nagyobb problémát kisebb problémákra, mint oldja meg a kisebb problémákat a nagyobb probléma megoldása érdekében. Ebben a cikkben a Merve Sorting Algorithms Java nyelvét tárgyaljuk. Fogalmi szempontból a Merge sort a MERGE és a MERGE_SORT nevű két alapalgoritmus kombinációja, amely a következőképpen működik:
- Ossza meg a válogatott listát n számú egyelemű allistára (n a válogatott listában szereplő összes elem száma).
- Az allistákat ismételten egyesítjük rendezett allistákba, amíg csak egy rendezett lista lesz.
Egyesítési rendezési algoritmusok megvalósítása Java-ban
A MERGE algoritmus a két rendezett lista egyetlen rendezett listává történő kombinálásának az eljárása.
Példa: Tegyük fel, hogy két lista létezik, azaz az 1. lista (6, 3) és a 2. lista (3, 1, 9).
1. Először rendezze el mindkét listát.
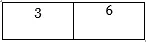
1. lista

2. lista
Most összevonási technikát alkalmazunk rajta.
- Ezután készítünk egy új, m + n méretű listát, ahol m az 1. listában szereplő elemek száma és n a 2. listában szereplő elemek száma.

3. lista
Esetünkben m = 2 és n = 3, tehát m + n = 5.
- Most van egy két mutatónk. Az első mutató az 1. lista első helyzetére mutat, és a második mutató a 2. lista első helyzetére mutat.
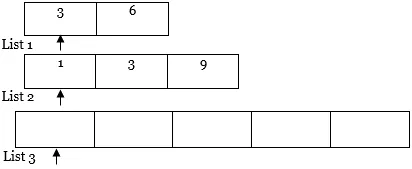
4. Ezután összehasonlítjuk mindkét mutató értékét. A kisebb értékű mutatót, másolja az elemet a 3. listába, és mozgassa az egérmutatót jobb oldalra a kisebb értékű és az ennek eredményeként létrejövő lista számára (azaz az 1. és a 3. lista).
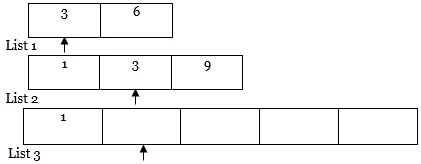
5. Hasonlóképpen hajtsa végre újra és újra a 4. lépést.
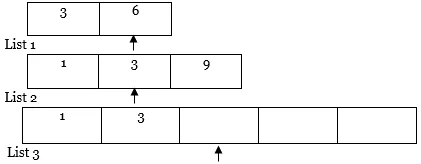
További út…
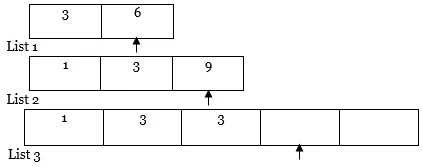
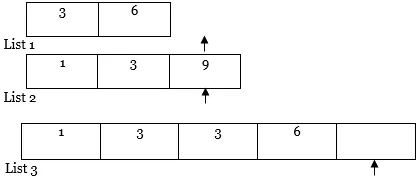
MEGJEGYZÉS: Ha az egyik lista (azaz az 1. vagy a 2. lista) teljes mértékben áthalad, mint a fenti esetben, akkor másolja a többi lista teljes tartalmát a mutatóról az eredménylistára (azaz a 3. listára) az alábbiak szerint.

Algoritmus és álnév
Az egyesítési algoritmusban alkalmazott két algoritmus a következő:
- A MERGE (ARR, F, M, L) olyan folyamat, amely feltételezi a következőket:
- ARR (F… .M) és ARR (M + 1… .L) rendezett listák.
- Egyesíti a két rendezett allistát egy ARR-be (F… .L).
- SORT (ARR (), F, L) // itt F az első, és L a tömb utolsó indexe.
Ha (L> 1)
- Keresse meg a középső pontot, hogy a listát két részre osztja:
középső M = (F + L) / 2
- Call Merge Sort az első félévben:
Hívja a SORT-ot (ARR, 1, M)
- Call Merge Sort a második felére:
Hívás SORT (ARR, M + 1, L)
- Egyesítse a 2. és 3. lépésben rendezett feleket:
Hívja a Merge (ARR, L, M, R)
Példa
Vegyünk példát egy ARR (10, 6, 8, 5, 7, 3, 4) tömbre. Az Összevonási algoritmust a tömb osztályozására használja a Divide and Conquer technika felhasználásával. Az alábbi ábrán láthatjuk, hogy a tömb rekurzív módon két részre van osztva, amíg a méret 1-ig nem lesz. Ha a méret 1-nek válik, akkor összevonási folyamatokat hívunk, és a listák egyesítését kezdjük újra, amíg a teljes lista össze nem merül.
MEGJEGYZÉS: Az alábbi ábrán a piros számok jelzik a lépések feldolgozási sorrendjét a Rendezett tömb létrehozásához.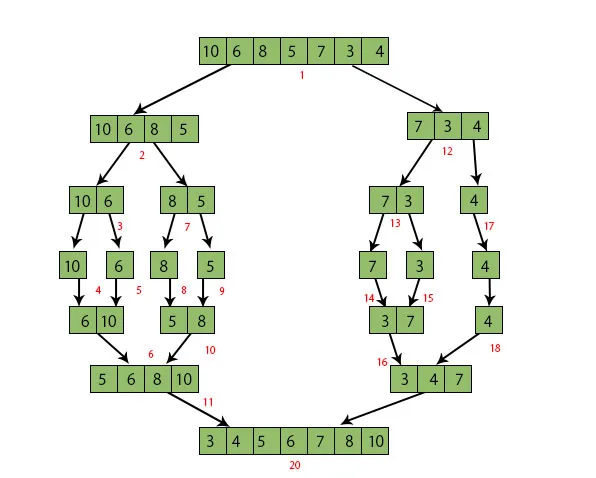
Program kód:
import java.util.Scanner;
public class mergeSort (
// merges two sublists of arr().
// first list is arr(l..m) // second list is arr(m+1..r) void mergeAlgo(int arr(), int l, int m, int r)
(
// find the sizes of two lists to be merged
int n1 = m - l + 1;
int n2 = r - m;
// create temp array
int L() = new int (n1);
int R() = new int (n2);
// copy data to temp arrays
for (int i=0; i L(i) = arr(l + i);
for (int j=0; j R(j) = arr(m + 1+ j);
/* merge the temp arrays */
// initial indexes of first and second list
int i = 0, j = 0;
// initial index of merged sub list
int k = l;
while (i < n1 && j < n2)
(
if (L(i) <= R(j))
(
arr(k) = L(i);
i++;
)
else
(
arr(k) = R(j);
j++;
)
k++;
)
// copy remaining elements of L() if any
while (i < n1)
(
arr(k) = L(i);
i++;
k++;
)
// copy remaining elements of R() if any
while (j < n2)
(
arr(k) = R(j);
j++;
k++;
)
)
// main function that sorts arr(l..r) using mergeAlgo()
void sort(int arr(), int l, int r)
(
if (l < r)
(
// find the middle index
int m = (l+r)/2;
// sort first and second halves
sort(arr, l, m);
sort(arr, m+1, r);
// merge the above two sorted halves
mergeAlgo(arr, l, m, r);
)
)
/* A function to print list of size n */
static void printArray(int arr())
(
int n = arr.length;
for (int i=0; i System.out.print(arr(i) + " ");
System.out.println();
)
public static void main(String args())
(
Scanner myObj = new Scanner(System.in);
System.out.println("Enter the size of list:");
int N = myObj.nextInt();
System.out.println("Enter the elements in list separated by space:");
int arr() = new int(N);
for(int i=0; i arr(i) = myObj.nextInt();
)
mergeSort mg = new mergeSort();
mg.sort(arr, 0, arr.length-1);
System.out.println("\nSorted list:");
printArray(arr);
)
)import java.util.Scanner;
public class mergeSort (
// merges two sublists of arr().
// first list is arr(l..m) // second list is arr(m+1..r) void mergeAlgo(int arr(), int l, int m, int r)
(
// find the sizes of two lists to be merged
int n1 = m - l + 1;
int n2 = r - m;
// create temp array
int L() = new int (n1);
int R() = new int (n2);
// copy data to temp arrays
for (int i=0; i L(i) = arr(l + i);
for (int j=0; j R(j) = arr(m + 1+ j);
/* merge the temp arrays */
// initial indexes of first and second list
int i = 0, j = 0;
// initial index of merged sub list
int k = l;
while (i < n1 && j < n2)
(
if (L(i) <= R(j))
(
arr(k) = L(i);
i++;
)
else
(
arr(k) = R(j);
j++;
)
k++;
)
// copy remaining elements of L() if any
while (i < n1)
(
arr(k) = L(i);
i++;
k++;
)
// copy remaining elements of R() if any
while (j < n2)
(
arr(k) = R(j);
j++;
k++;
)
)
// main function that sorts arr(l..r) using mergeAlgo()
void sort(int arr(), int l, int r)
(
if (l < r)
(
// find the middle index
int m = (l+r)/2;
// sort first and second halves
sort(arr, l, m);
sort(arr, m+1, r);
// merge the above two sorted halves
mergeAlgo(arr, l, m, r);
)
)
/* A function to print list of size n */
static void printArray(int arr())
(
int n = arr.length;
for (int i=0; i System.out.print(arr(i) + " ");
System.out.println();
)
public static void main(String args())
(
Scanner myObj = new Scanner(System.in);
System.out.println("Enter the size of list:");
int N = myObj.nextInt();
System.out.println("Enter the elements in list separated by space:");
int arr() = new int(N);
for(int i=0; i arr(i) = myObj.nextInt();
)
mergeSort mg = new mergeSort();
mg.sort(arr, 0, arr.length-1);
System.out.println("\nSorted list:");
printArray(arr);
)
)import java.util.Scanner;
public class mergeSort (
// merges two sublists of arr().
// first list is arr(l..m) // second list is arr(m+1..r) void mergeAlgo(int arr(), int l, int m, int r)
(
// find the sizes of two lists to be merged
int n1 = m - l + 1;
int n2 = r - m;
// create temp array
int L() = new int (n1);
int R() = new int (n2);
// copy data to temp arrays
for (int i=0; i L(i) = arr(l + i);
for (int j=0; j R(j) = arr(m + 1+ j);
/* merge the temp arrays */
// initial indexes of first and second list
int i = 0, j = 0;
// initial index of merged sub list
int k = l;
while (i < n1 && j < n2)
(
if (L(i) <= R(j))
(
arr(k) = L(i);
i++;
)
else
(
arr(k) = R(j);
j++;
)
k++;
)
// copy remaining elements of L() if any
while (i < n1)
(
arr(k) = L(i);
i++;
k++;
)
// copy remaining elements of R() if any
while (j < n2)
(
arr(k) = R(j);
j++;
k++;
)
)
// main function that sorts arr(l..r) using mergeAlgo()
void sort(int arr(), int l, int r)
(
if (l < r)
(
// find the middle index
int m = (l+r)/2;
// sort first and second halves
sort(arr, l, m);
sort(arr, m+1, r);
// merge the above two sorted halves
mergeAlgo(arr, l, m, r);
)
)
/* A function to print list of size n */
static void printArray(int arr())
(
int n = arr.length;
for (int i=0; i System.out.print(arr(i) + " ");
System.out.println();
)
public static void main(String args())
(
Scanner myObj = new Scanner(System.in);
System.out.println("Enter the size of list:");
int N = myObj.nextInt();
System.out.println("Enter the elements in list separated by space:");
int arr() = new int(N);
for(int i=0; i arr(i) = myObj.nextInt();
)
mergeSort mg = new mergeSort();
mg.sort(arr, 0, arr.length-1);
System.out.println("\nSorted list:");
printArray(arr);
)
)import java.util.Scanner;
public class mergeSort (
// merges two sublists of arr().
// first list is arr(l..m) // second list is arr(m+1..r) void mergeAlgo(int arr(), int l, int m, int r)
(
// find the sizes of two lists to be merged
int n1 = m - l + 1;
int n2 = r - m;
// create temp array
int L() = new int (n1);
int R() = new int (n2);
// copy data to temp arrays
for (int i=0; i L(i) = arr(l + i);
for (int j=0; j R(j) = arr(m + 1+ j);
/* merge the temp arrays */
// initial indexes of first and second list
int i = 0, j = 0;
// initial index of merged sub list
int k = l;
while (i < n1 && j < n2)
(
if (L(i) <= R(j))
(
arr(k) = L(i);
i++;
)
else
(
arr(k) = R(j);
j++;
)
k++;
)
// copy remaining elements of L() if any
while (i < n1)
(
arr(k) = L(i);
i++;
k++;
)
// copy remaining elements of R() if any
while (j < n2)
(
arr(k) = R(j);
j++;
k++;
)
)
// main function that sorts arr(l..r) using mergeAlgo()
void sort(int arr(), int l, int r)
(
if (l < r)
(
// find the middle index
int m = (l+r)/2;
// sort first and second halves
sort(arr, l, m);
sort(arr, m+1, r);
// merge the above two sorted halves
mergeAlgo(arr, l, m, r);
)
)
/* A function to print list of size n */
static void printArray(int arr())
(
int n = arr.length;
for (int i=0; i System.out.print(arr(i) + " ");
System.out.println();
)
public static void main(String args())
(
Scanner myObj = new Scanner(System.in);
System.out.println("Enter the size of list:");
int N = myObj.nextInt();
System.out.println("Enter the elements in list separated by space:");
int arr() = new int(N);
for(int i=0; i arr(i) = myObj.nextInt();
)
mergeSort mg = new mergeSort();
mg.sort(arr, 0, arr.length-1);
System.out.println("\nSorted list:");
printArray(arr);
)
)import java.util.Scanner;
public class mergeSort (
// merges two sublists of arr().
// first list is arr(l..m) // second list is arr(m+1..r) void mergeAlgo(int arr(), int l, int m, int r)
(
// find the sizes of two lists to be merged
int n1 = m - l + 1;
int n2 = r - m;
// create temp array
int L() = new int (n1);
int R() = new int (n2);
// copy data to temp arrays
for (int i=0; i L(i) = arr(l + i);
for (int j=0; j R(j) = arr(m + 1+ j);
/* merge the temp arrays */
// initial indexes of first and second list
int i = 0, j = 0;
// initial index of merged sub list
int k = l;
while (i < n1 && j < n2)
(
if (L(i) <= R(j))
(
arr(k) = L(i);
i++;
)
else
(
arr(k) = R(j);
j++;
)
k++;
)
// copy remaining elements of L() if any
while (i < n1)
(
arr(k) = L(i);
i++;
k++;
)
// copy remaining elements of R() if any
while (j < n2)
(
arr(k) = R(j);
j++;
k++;
)
)
// main function that sorts arr(l..r) using mergeAlgo()
void sort(int arr(), int l, int r)
(
if (l < r)
(
// find the middle index
int m = (l+r)/2;
// sort first and second halves
sort(arr, l, m);
sort(arr, m+1, r);
// merge the above two sorted halves
mergeAlgo(arr, l, m, r);
)
)
/* A function to print list of size n */
static void printArray(int arr())
(
int n = arr.length;
for (int i=0; i System.out.print(arr(i) + " ");
System.out.println();
)
public static void main(String args())
(
Scanner myObj = new Scanner(System.in);
System.out.println("Enter the size of list:");
int N = myObj.nextInt();
System.out.println("Enter the elements in list separated by space:");
int arr() = new int(N);
for(int i=0; i arr(i) = myObj.nextInt();
)
mergeSort mg = new mergeSort();
mg.sort(arr, 0, arr.length-1);
System.out.println("\nSorted list:");
printArray(arr);
)
)
Kimenet:
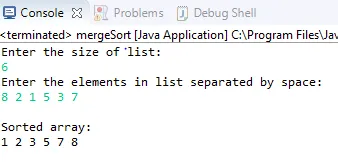
Következtetés - Rendezési algoritmusok egyesítése Java-ban
Az egyesítési sorrendben a legjobb, a legrosszabb és az átlagos esetek komplexitása azonos, ami hatékonyabb algoritmust eredményez. Gyorsabban működik, mint más válogatási technikák. Az egyesítés sort bármilyen méretű fájlra alkalmazható. Nagyon párhuzamosítható az osztás és hódítás módszer alkalmazásának köszönhetően. A számítástechnika alapjainak fejlesztése érdekében tanácsos alaposan megérteni a különféle rendezési algoritmusokat.
Ajánlott cikkek
Ez egy útmutató a Java szortírozási algoritmusok egyesítéséhez. Itt példázzuk az egyesítési rendezési algoritmusok Java alkalmazásban, valamint az algoritmusban és álkódban történő megvalósítását. Megnézheti más javasolt cikkeinket is -
- Kiválasztás Rendezés Java-ban
- Esetnyilatkozat Java-ban
- Hozzáférés a Java módosítóihoz
- Merge Rendezés a JavaScript-ben
- Mi az esettanulmány a JavaScript-ben?
- Hozzáférés-módosítók a PHP-ben
- Gyors rendezési algoritmusok a Java-ban
- Teljes útmutató a C # szerinti rendezéshez, példákkal
- Rendezési funkció Python-ban példákkal
- A 6 legnépszerűbb rendezési algoritmus a JavaScript-ben