
Bevezetés a binomiális eloszlásba R
Ez a cikk leírja, hogyan lehet a binomiális eloszlásokat felhasználni az R-ben a néhány valószínűség-eloszlású művelethez. Az üzleti elemzés a binomiális valószínűséget használja egy összetett probléma megoldására. Az R számos beépített funkcióval rendelkezik a statisztikai interferenciákhoz használt binomiális eloszlások kiszámításához. A binomiális eloszlás, más néven Bernoulli-kísérletek: kétfajta p és bukási sikert vesz igénybe. A binomiális eloszlási modell fő célja az, hogy a lehetséges valószínűségi eredményeket kiszámítsák egy meghatározott pozitív lehetőség megfigyelésével, a folyamat bizonyos számú megismétlésével. . Két lehetséges eredménynek kell lennie (siker / kudarc), ezért az eredmény kettős. Az előre meghatározott matematikai jelölés p = siker, q = 1-p.
A binomiális eloszlásokhoz négy funkció kapcsolódik. Ezek dbinom, pbinom, qbinom, rbinom. A formázott szintaxist az alábbiakban adjuk meg:
Szintaxis
- dbinom (x, méret, prob)
- pbinom (x, méret, prob)
- qbinom (x, méret, prob) vagy qbinom (x, méret, prob, alsó_szög, log_p)
- rbinom (x, méret, prob)
A függvénynek három érve van: az x érték a kvantumok vektorja (0-tól n-ig), a méret a nyomvonalak kísérletének száma, a prob minden egyes kísérlet valószínűségét jelöli. Nézzük meg egyenként egy példát.
1) dbinom ()
Ez egy sűrűség vagy eloszlási függvény. A vektor értékeknek egész számnak kell lenniük, nem szabad negatív számnak lennie. Ez a funkció számos sikert próbál meg találni a nem értékkel. a rögzített vizsgálatok száma.
A binomiális eloszlás figyelembe veszi a méretet és az x értékeket. Például, méret = 6, a lehetséges x értékek 0, 1, 2, 3, 4, 5, 6, ami P (X = x) -re utal.
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
Kimenet:
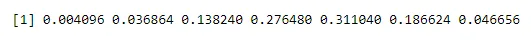
Az egyik valószínűsége
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
Kimenet:
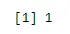
1. példa - A kórházi adatbázis azt mutatja, hogy a rákban szenvedő betegek 65% -a hal meg. Mi lesz annak valószínűsége, hogy 5 véletlenszerűen kiválasztott beteg közül három közül felépül?
Itt alkalmazzuk a dbinom függvényt. Annak valószínűsége, hogy 3 helyrehozza az összes pont sűrűség eloszlását.
n = 5, p = 0, 65, x = 3
dbinom(3, size=5, prob=0.65)
Kimenet:

X érték 0-tól 3-ig:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
Kimenet:
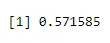
Ezután készítsen egy 40 papírból álló mintát, és 2-kel növelje meg a binomiált a dbinom használatával.
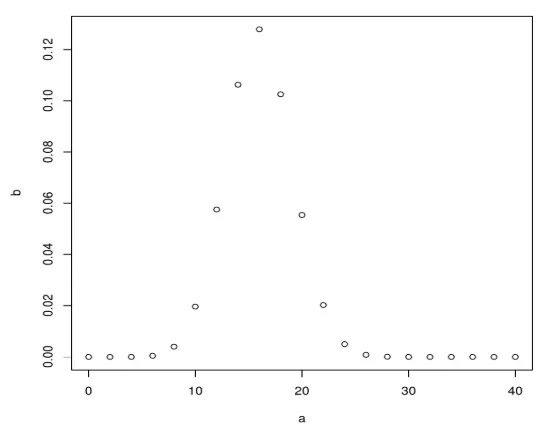
a <- seq(0, 40, by = 2)
b <- dbinom(a, 40, 0.4)
plot(a, b)
A fenti kód végrehajtása után a következő kimenetet állítja elő: A binomiális eloszlást plot () függvény segítségével ábrázoljuk.
2. példa - Vegyünk egy forgatókönyvet, tegyük fel, hogy annak a valószínűsége, hogy egy hallgató könyvtárat kölcsönöz egy könyvtárból, 0, 7. 6 hallgató van a könyvtárban, mi a valószínűsége annak, hogy közülük 3 kölcsönz egy könyvet?
itt P (X = 3)
Kód:
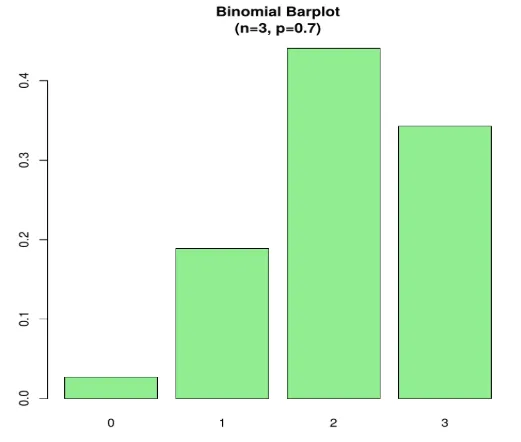
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
A Plot alatt látható, ha p> 0, 5, ezért a binomiális eloszlás pozitívan ferde a megjelenítettnél.
Kimenet:
2) Pbinom ()
kiszámítja a binomiális vagy a CDF kumulatív valószínűségét (P (X <= x)).
1. példa:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
Kimenet:

2. példa: Dravid gömbölyít a kaput a kísérleteinek 20% -ára, amikor tálat dob. Ha ötször dobál, milyen valószínűséggel kap 4 vagy annál kevesebb kiskapu?
A siker valószínűsége itt 0, 2, és öt kísérlet során megkapjuk
pbinom(4, size=5, prob=.2)
Kimenet:
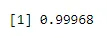
3. példa: Az amerikaiak 4% -a fekete. Keresse meg a 2 fekete hallgató valószínűségét, ha véletlenszerűen választ ki 6 hallgatót a 100 osztályból pótlás nélkül.
Ha R: x = 4 R: n = 6 R: p = 0 0 4
pbinom(4, 6, 0.04)
Kimenet:-
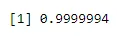
3) qbinom ()
Ez egy kvantitatív függvény, és a kumulatív valószínűségfüggvény inverzét adja meg. Az összesített érték megegyezik egy valószínűségi értékkel.
Példa: Hány farok valószínűsége 0, 2, ha egy érmét 61 alkalommal dobnak el.
a <- qbinom(0.2, 61, 1/2)
print(a)
Kimenet:-
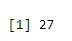
4) rbinom ()
Véletlen számokat generál. A különböző eredmények különböző véletlenszerű outputot eredményeznek, amelyeket a szimulációs folyamatban használnak.
Példa:-
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Kimenet:-

Minden alkalommal, amikor végrehajtjuk, véletlenszerű eredményeket ad.
rbinom(200, 4, 0.4)
Kimenet:-

Itt csináljuk ezt úgy, ha feltételezzük, hogy 30 érmecsapás eredménye egyetlen kísérlettel történik.
rbinom(30, 1, 0.5)
Kimenet:-
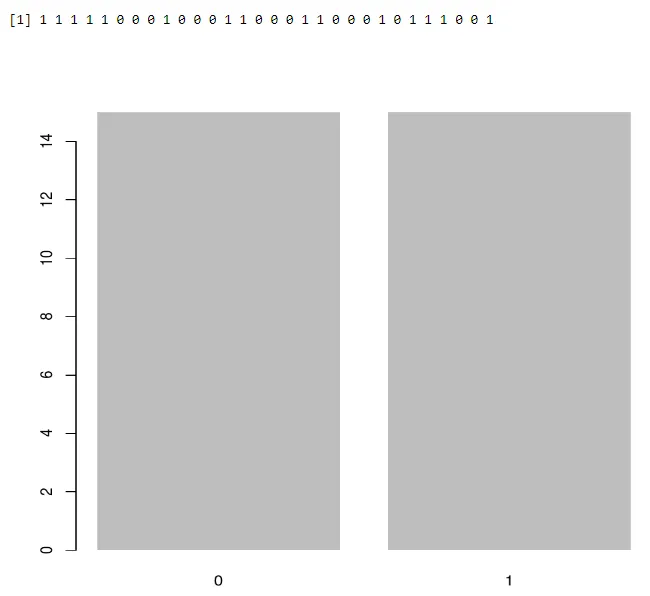
A barplot használata:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Kimenet:-
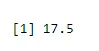
Hogy megtaláljuk a siker közepette
output <-rbinom(10, size=60, 0.3)
mean(output)
Kimenet:-
Következtetés - Binomiális eloszlás az R-ben
Ezért ebben a dokumentumban megvitattuk a binomiális eloszlást R-ben. Különféle példákkal szimuláltuk az R stúdióban és az R kivonatokban leírtakot, és a beépített függvények leírását is segítik a binomiális számítások generálásában. Az R binomiális eloszlásának számítása statisztikai számításokat használ. Ezért egy binomiális eloszlás segítséget nyújt a valószínűség és a véletlenszerű keresés megtalálásában egy binomiális változó segítségével.
Ajánlott cikkek
Ez egy útmutató a Binomiális eloszláshoz R. Itt tárgyaljuk a bevezetést és annak a Binomiális eloszláshoz kapcsolódó funkcióit, a szintaxist és a megfelelő példákat. A további javasolt cikkeken keresztül további információkat is megtudhat -
- Binomiális eloszlásképlet
- Közgazdaságtan vs üzleti
- Üzleti elemzési technikák
- Linux disztribúciók